题目内容

在△ABC中，已知AB=2，C=
π
3
，求△ABC的周长的最大值．
考点：正弦定理
专题：三角函数的图像与性质
分析：由三角形的知识可得△ABC的周长=AB+AC+BC=2+
4
3
sinB+
4
3
sinA=2+
4
3
sin（
2π
3
-A）+
4
3
sinA，化简结合A的范围可得答案．
解答： 解：由正弦定理可得
2
sin
π
3
=
AC
sinB
=
BC
sinA
，
变形可得AC=
4
3
sinB，BC=
4
3
sinA，
∴△ABC的周长=AB+AC+BC=2+
4
3
sinB+
4
3
sinA
=2+
4
3
sin（
2π
3
-A）+
4
3
sinA
=2+4sin（A+
π
6
），
∵A∈（0，
2π
3
），∴A+
π
6
∈（
π
6
，
5π
6
），
∴sin（A+
π
6
）∈（
1
2
，1]
∴当sin（A+
π
6
）=1时，△ABC的周长2+4sin（A+
π
6
）取最大值6
点评：本题考查三角函数的最值，涉及正弦定理的应用，属基础题．
练习册系列答案
相关题目
若数列{an}满足：a1=19，an+1=an-2（n∈N+），则数列{an}的前n项和最大时，n的值是（　　）
A、9B、10C、11D、12
对于实数a、b、c有如下命题①若a＞b则ac＞bc；②若ac2＞bc2则a＞b；③若a＜b＜0则a2＞ab＞b2；④若a＞b，
1
a
＞
1
b
则a＞0，b＜0．其中正确的有（　　）
A、1个B、2个C、3个D、4个
下列计算：①（-2014）0=1；②2m-4=
1
2m4
；③x4+x3=x7；④（ab2）3=a3b6；⑤
(-35)2
=35，正确的是（　　）
A、①B、①②③
C、①③④D、①④⑤
设
a
，
b
是两个非零向量，则下列命题正确的是（　　）
A、若
a
⊥
b
，则|
a
-
b
|=|
a
|+|
b
|
B、若|
a
-
b
|=|
a
|+|
b
|，则
a
⊥
b
C、若存在实数λ，使得
a
=λ
b
，则|
a
-
b
|=|
a
|+|
b
|
D、若|
a
-
b
|=|
a
|+|
b
|，则存在实数λ，使得
a
=λ
b
解关于x的不等式：x2+3x+2≤0．
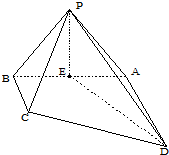如图，四棱锥P-ABCD中，底面ABCD是直角梯形，∠DAB=90°，AD∥BC，AD⊥侧面PAB，△PAB是等边三角形，DA=AB=2=0，BC=
1
2
AD，E是线段AB的中点．
（1）求证：PE⊥CD；
（2）F为线段PC的中点，求平面PBC与平面DEF所成锐二面角的平面角的余弦值．
将函数y=sinx的图象向右平移
π
3
个单位，再将所得图象上各点的横坐标不变，纵坐标伸长到原来的4倍，这样就得到函数f（x）的图象，若g（x）=f（x）cosx+
3
．
（1）将函数表示为g（x）=Asin（ωx+φ）+B（其中A，ω＞0，φ∈[-
π
2
，
π
2
]）的形式；
（2）若函数g（x）在区间[-
π
12
，θ]上的最大值为2，求θ的最小值．
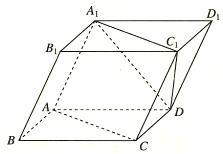如图，棱柱ABCD-A1B1C1D1的所有棱长都等于2，∠ABC=∠A1AC=60°，平面AA1CC1⊥平面ABCD．
（1）证明：BD⊥AA1；
（2）求三棱锥A-DCC1的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网