题目内容
12.函数$y=sin(wx+\frac{π}{3})$ 的最小正周期为$\frac{π}{2}$,则正数w 的值为4.分析 由条件利用正弦函数的周期性,求得正数w 的值.
解答 解:函数$y=sin(wx+\frac{π}{3})$ 的最小正周期为$\frac{2π}{w}$=$\frac{π}{2}$,则正数w=4,
故答案为:4.
点评 本题主要考查正弦函数的周期性,属于基础题.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
20.已知椭圆$\frac{x^2}{16}+\frac{y^2}{12+m}=1的离心率e=\frac{{\sqrt{2}}}{2}$实数m为( )
| A. | -4或16 | B. | 20 | C. | -4或20 | D. | -4 |
7.设正实数x,y满足x>$\frac{1}{2}$,y>1,不等式$\frac{4{x}^{2}}{y-1}$+$\frac{{y}^{2}}{2x-1}$≥m恒成立,则m的最大值为( )
| A. | 2$\sqrt{2}$ | B. | 4$\sqrt{2}$ | C. | 8 | D. | 16 |
1.在△ABC,已知a:b:c=3:5:7,则这个三角形最大角的外角是( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
2.函数f(x)=x3-3x2-7x+a的图象与直线y=2x+1相切,则a=( )
| A. | 28或4 | B. | 28或-4 | C. | -28或4 | D. | -28或-4 |
 中,
中, ,点
,点 是
是 的中点.
的中点.
 ;
; 平面
平面 .
.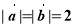 ,向量
,向量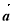 与
与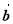 的夹角为
的夹角为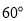 ,则
,则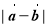 等于( )
等于( )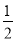 B.
B.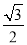 C.2 D.4
C.2 D.4 为了了解一种植物果实的情况,随机抽取一批该植物果实样本测量重量(单位:克),按照[27.5,32.5),[32.5,37.5),[37.5,42.5),[42.5,47.5),[47.5,52.5]分为5组,其频率分布直方图如图所示.
为了了解一种植物果实的情况,随机抽取一批该植物果实样本测量重量(单位:克),按照[27.5,32.5),[32.5,37.5),[37.5,42.5),[42.5,47.5),[47.5,52.5]分为5组,其频率分布直方图如图所示.