题目内容
已知数列{an}满足的前n项和为Sn,且Sn=(
)n+n-1,(n∈N*).
(1)求数列{an}的通项公式;
(2)若数列{bn}的通项公式满足bn=n(1-an),求数列{bn}的前n项和Tn.
| 1 |
| 3 |
(1)求数列{an}的通项公式;
(2)若数列{bn}的通项公式满足bn=n(1-an),求数列{bn}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用数列的前n项和,通过Sn-Sn-1=an求出数列的通项公式.
(2)化简数列{bn}的通项公式bn=n(1-an),利用错位相减法求解数列的和即可.
(2)化简数列{bn}的通项公式bn=n(1-an),利用错位相减法求解数列的和即可.
解答:
解:(1)由,Sn=(
)n+n-1,(n∈N*)
当n=1时得a1=S1=
,当n≥2时得an=Sn-Sn-1=1-
,
又a1=
满足上式,所以:数列{an}的通项公式为an=1-
.
(2)由bn=n(1-an)=
.
所以Tn=
+
+
+…+
,
得
Tn=
+
+
+…+
相减得:
Tn=2(
+
+
+…+
-
)
∴Tn=
-
.
| 1 |
| 3 |
当n=1时得a1=S1=
| 1 |
| 3 |
| 2 |
| 3n |
又a1=
| 1 |
| 3 |
| 2 |
| 3n |
(2)由bn=n(1-an)=
| 2n |
| 3n |
所以Tn=
| 2•1 |
| 3 |
| 2•2 |
| 32 |
| 2•3 |
| 33 |
| 2n |
| 3n |
得
| 1 |
| 3 |
| 2•1 |
| 32 |
| 2•2 |
| 33 |
| 2•3 |
| 34 |
| 2n |
| 3n+1 |
相减得:
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 33 |
| 1 |
| 3n |
| n |
| 3n+1 |
∴Tn=
| 3 |
| 2 |
| 2n+3 |
| 2•3n |
点评:本题考查数列通项公式的求法,数列的和的求法,错位相减法的应用,考查计算能力.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
一个几何体的三视图如图所示,则该几何体的体积是( )


| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
下列说法正确的是( )
| A、样本10,6,8,5,6的标准差是3.3. | ||||
| B、“p∨q为真”是“p∧q为真”的充分不必要条件 | ||||
| C、已知点A(-2,1)在抛物线y2=2px(p>0)的准线上,记其焦点为F,则直线AF的斜率等于-4 | ||||
D、设有一个回归直线方程为
|
下列说法错误的是( )
| A、命题p“?x∈R,ax>0(a>0且a≠1),则¬p:?x0∈R,ax0≤0 |
| B、如果命题“¬p”与命题“p或q”都是真命题,那么命题q一定是真命题 |
| C、特称命题“?x∈R,使-2x2+x-4=0”是假命题 |
| D、命题“若a,b都是偶数,则a+b是偶数”的否命题是“若a,b都不是偶数,则a+b不是偶数” |
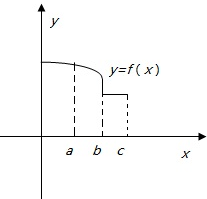 函数y=f(x)的图象如图所示,试画出导函数f′(x)的大致形状.
函数y=f(x)的图象如图所示,试画出导函数f′(x)的大致形状. 已知某几何体的侧视图与其正视图相同,相关的尺寸如图所示,则这个几何体的表面积是
已知某几何体的侧视图与其正视图相同,相关的尺寸如图所示,则这个几何体的表面积是