题目内容
15.设函数f(x)=(x+2)ex.(1)求f(x)的单调区间;
(2)当x≥0时,恒有$\frac{f(x)-{e}^{x}}{ax+1}$≥1,求实数a的取值范围.
分析 (1)求出函数f(x)的导数,解关于导函数的不等式,求出函数的单调区间即可;
(2)通过讨论a的范围,结合函数的单调性确定a的具体范围即可.
解答 解:(1)f′(x)=(x+3)ex,
令f′(x)>0,解得:x>-3,令f′(x)<0,解得:x<-3,
故函数f(x)在(-∞,-3)递减,在(-3,+∞)递增;
(2)a<0时,若x>-$\frac{1}{a}$,则$\frac{x+1}{ax+1}$ex<0,${\frac{x+1}{ax+1}e}^{x}≥1$不成立,
当a≥0时,记g(x)=(x+1)ex-ax-1,则$\frac{x+1}{ax+1}$ex≥1当且仅当g(x)≥0,
g′(x)=(x+2)ex-a,
当x≥0时,(x+2)ex≥2,当0≤a≤2时,g′(x)≥0,
故g(x)在[0,+∞)递增,故g(x)≥g(0)=0,
a>2时,由(1)知g′(x)在[0,+∞)递增,且g′(0)=2-a<0,
g′(a-2)=a(ea-2-1)>0,于是,g′(x)=0在[0,+∞)上有且只有1个实根,
不妨设该实根为x0,当0<x<x0时,g′(x)<0,从而g(x)在(0,x0)递减,
故x∈(0,x0)时,g(x)<g(0)=0,不合题意,
综上,实数a的范围是[0,2].
点评 本题考查了函数的单调性问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
5.已知圆锥的表面积等于12πcm2,其侧面展开图是一个半圆,则底面圆的半径为( )
| A. | 1cm | B. | 2cm | C. | 3cm | D. | $\frac{3}{2}cm$ |
3.已知A(2,0),B(3,$-\sqrt{3}$),直线 l∥AB,则直线l的倾斜角为( )
| A. | 135° | B. | 120° | C. | 60° | D. | 45° |
20.一位同学一次投篮的命中率试0.4,我们通过随机模拟的方式来判断这位同学3次投篮的命中情况,用表示命中,用0,1,2,3表示不命中,计算机产生20组随机数:
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
则这位同学恰有两次命中的概率是( )
907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
则这位同学恰有两次命中的概率是( )
| A. | $\frac{7}{20}$ | B. | $\frac{9}{20}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
20.在等差数列{an}中,a3+a6+a9=54,设数列{an}的前n项和为Sn,则S11=( )
| A. | 18 | B. | 99 | C. | 198 | D. | 297 |
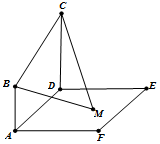 已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2.ADEF是正方形,在正方形ADEF内部有一点M,满足MB,MC与平面ADEF所成的角相等,则点M的轨迹长度为$\frac{4}{9}$π.
已知平面ABCD⊥平面ADEF,AB⊥AD,CD⊥AD,且AB=1,AD=CD=2.ADEF是正方形,在正方形ADEF内部有一点M,满足MB,MC与平面ADEF所成的角相等,则点M的轨迹长度为$\frac{4}{9}$π.