题目内容
【题目】如图,已知椭圆C: ![]() 的右顶点为A,离心率为e,且椭圆C过点
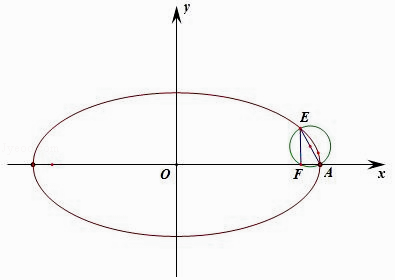
的右顶点为A,离心率为e,且椭圆C过点 ![]() ,以AE为直径的圆恰好经过椭圆的右焦点.
,以AE为直径的圆恰好经过椭圆的右焦点.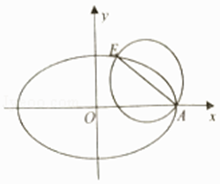
(1)求椭圆C的标准方程;
(2)已知动直线l(直线l不过原点且斜率存在)与椭圆C交于P,Q两个不同的点,且△OPQ的面积S=1,若N为线段PQ的中点,问:在x轴上是否存在两个定点E1 , E2 , 使得直线NE1与NE2的斜率之积为定值?若存在,求出E1 , E2的坐标;若不存在,说明理由.
【答案】
(1)
解:连接EF,则EF⊥FA,则xF=c=2e,则c= ![]() ,解得:a=2,
,解得:a=2,
故点E(c, ![]() ),代入椭圆方程:
),代入椭圆方程: ![]() ,解得:c=
,解得:c= ![]() ,
,
b2=a2﹣c2=1,
故椭圆的方程: ![]()
(2)
解:设直线l的方程为:y=kx+m,P(x1,y1),Q(x2,y2),
则 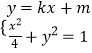 ,整理得:(1+4k2)x2+8kmx+4m2=4=0,
,整理得:(1+4k2)x2+8kmx+4m2=4=0,
x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
则丨PQ丨= ![]() =
= ![]() ,
,
原点到直线l的距离d= ![]() ,
,
∴△OPQ的面积S△OPQ= ![]() 丨PQ丨×d=
丨PQ丨×d= ![]() ×
× ![]() =1,
=1,
即2丨m丨 ![]() =1+4k2,则1+4k2=2m2,
=1+4k2,则1+4k2=2m2,
设N(x,y),则x= ![]() =﹣
=﹣ ![]() =﹣
=﹣ ![]() ,y=
,y= ![]() =
= ![]() =
= ![]() ,
,
由①,②消去m, ![]() ,
,
假设x轴上,存在两定点E1(s,0),E2(t,0),(s≠t)
那么直线NE1的斜率k1= ![]() ,直线NE2的斜率k2=
,直线NE2的斜率k2= ![]() ,
,
则k1k2= ![]() =﹣
=﹣ ![]() ,
,
当且仅当s+t=0,st=﹣2,k1k2=﹣ ![]() ,解得:s=
,解得:s= ![]() ,t=﹣
,t=﹣ ![]() ,
,
即存在定点E1( ![]() ,0),E2(﹣
,0),E2(﹣ ![]() ,0),满足题意.
,0),满足题意.
【解析】(1)由题意可知c=2e,根据椭圆的离心率公式,即可求得a,将E代入椭圆方程,即可求得椭圆方程;(2)将直线方程代入椭圆方程,利用韦达定理及弦长公式,由S=1,求得1+4k2=2m2 , 设两点坐标,利用斜率公式,即可求得两点坐标.