题目内容
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且 ![]() .
.
(1)求sinB的值;
(2)若D为AC的中点,且BD=1,求△ABD面积的最大值.
【答案】
(1)解:由 ![]() .
.
可得: ![]()
由正弦定理: ![]() .
.
得: ![]() .即cosB=
.即cosB= ![]() .
.
那么:sinB= ![]()
(2)解:由BD=1,运用向量的关系,可得| ![]() |=2|
|=2| ![]() |=2,
|=2,
可得:| ![]() |2+|
|2+| ![]() |2+2
|2+2 ![]() =4,
=4,
则| ![]() |2+|
|2+| ![]() |2+2|
|2+2| ![]() |cosB=4,
|cosB=4,
由余弦定理:得| ![]() |2+|
|2+| ![]() |2=4﹣
|2=4﹣ ![]() ×|
×| ![]() |
|
∵| ![]() |2+|
|2+| ![]() |2≥2|
|2≥2| ![]() ||
|| ![]() |,(当且仅当|
|,(当且仅当| ![]() |=|
|=| ![]() |时取等号)
|时取等号)
∴4﹣ ![]() ×|
×| ![]() |≥2|
|≥2| ![]() ||
|| ![]() |,
|,
∴| ![]() ||
|| ![]() |≤
|≤ ![]() .
.
∴△ABC面积S= ![]() |
| ![]() ||
|| ![]() |sinB≤
|sinB≤ ![]() =
= ![]()
那么:△ABD面积的最大值为 ![]() =
= ![]() .
.
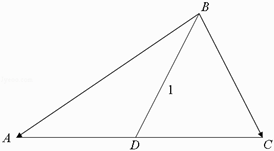
【解析】(1)运用正弦定理和三角形的内角和定理可得cosB,即可得sinB的值.(2)由BD=1,运用向量的关系可得| ![]() |=2|
|=2| ![]() |=2,平方后,可得|
|=2,平方后,可得| ![]() |2+|
|2+| ![]() |2+2
|2+2 ![]() =4利用基本不等式即可求解△ABD面积的最大值.
=4利用基本不等式即可求解△ABD面积的最大值.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() .
.

练习册系列答案
相关题目