Question

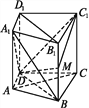
【题目】如图,在直四棱柱ABCD-A1B1C1D1中,DB=BC,DB⊥AC,点M是棱BB1上一点.

(1)求证:B1D1∥平面A1BD;

(2)求证:MD⊥AC;

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】试题分析：（1）在平面A1BD内找到和B1D1平行的直线BD即可．利用线线平行来推线面平行；（2）先利用条件BB1⊥AC和BD⊥AC证得AC⊥面BB1D，再证明MD⊥AC即可；（3）因为棱BB1上最特殊的点是中点，所以先看中点．取DC的中点N，D1C1的中点N1，连接NN1交DC1于O，BN⊥DC面ABCD⊥面DCC1D1，BN⊥面DCC1D1．而又可证得BN∥OM，所以可得OM⊥平面CC1D1D平面DMC1⊥平面CC1D1D．

详解：（1）证明：由直四棱柱，得BB1∥DD1且BB1=DD1，所以BB1D1D是平行四边形，

所以B1D1∥BD．

而BD平面A1BD，B1D1平面A1BD，

所以B1D1∥平面A1BD．

（2）证明：因为BB1⊥面ABCD，AC面ABCD，所以BB1⊥AC，

又因为BD⊥AC，且BD∩BB1=B，

所以AC⊥面BB1D，

而MD面BB1D，所以MD⊥AC．

（3）当点M为棱BB1的中点时，平面DMC1⊥平面CC1D1D

取DC的中点N，D1C1的中点N1，连接NN1交DC1于O，连接OM．

因为N是DC中点，BD=BC，所以BN⊥DC；又因为DC是面ABCD与面DCC1D1的交线，而面ABCD⊥面DCC1D1，

所以BN⊥面DCC1D1．

又可证得，O是NN1的中点，所以BM∥ON且BM=ON，即BMON是平行四边形，所以BN∥OM，所以OM⊥平面CC1D1D，因为OM面DMC1，所以平面DMC1⊥平面CC1D1D．