Question

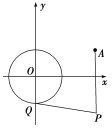
【题目】在平面直角坐标系中，定义两点A（xA ， yA），B（xB ， yB）间的“L﹣距离”为d（A﹣B）=|xA﹣xB|+|yA﹣yB|．现将边长为1的正三角形按如图所示方式放置，其中顶点A与坐标原点重合，记边AB所在的直线斜率为k（0≤k≤ ），则d（B﹣C）取得最大值时，边AB所在直线的斜率为 ．

Answer 1

【答案】2-
【解析】解：设B（cosθ，sinθ），则C（cos（θ+ ），sin（θ+ ）），
∴|BC|=|cos（θ+ ）﹣cosθ|+|sin（θ+ ）﹣sinθ|，
∵0≤θ≤ ，
∴ ≤θ+ ≤ ＜π，即0≤θ＜θ+ ＜π，
∴|cos（θ+ ）﹣cosθ|=cosθ﹣cos（θ+ ）．
∵0≤θ≤ ， ≤θ+ ≤ ，
∴|sin（θ+ ）﹣sinθ|=sin（θ+ ）﹣sinθ，
|BC|=cosθ﹣cos（θ+ ）+sin（θ+ ）﹣sinθ
=cosθ﹣cosθcos +sinθsin +sinθcos +cosθsin ﹣sinθ
= sinθ+ cosθ
= sin（θ+φ）（tanφ=2+ ），
由θ+φ= 2kπ，k∈Z，得θ=﹣φ+ 2kπ，k∈Z，
∴tanθ=tan（﹣φ+ 2kπ）= ，即边AB所在直线的斜率为2- 时，则d（B﹣C）取得最大值，
所以答案是2- ．
【考点精析】通过灵活运用直线的斜率，掌握一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα即可以解答此题．