Question

【题目】如图，在△ABC中，AB=2，cosB= ，点D在线段BC上．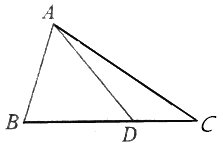

（1）若∠ADC= π，求AD的长；
（2）若BD=2DC，△ACD的面积为 ，求 的值．

Answer 1

【答案】
（1）解：∵△ABC中，cosB= ，∴sinB= ．

∵∠ADC= π，∴∠ADB= ．

△ABD中，由正弦定理可得 ，∴AD= ；

（2）解：设DC=a，则BD=2a，

∵BD=2DC，△ACD的面积为 ，

∴4 = ，

∴a=2

∴AC= =4 ，

由正弦定理可得 ，∴sin∠BAD= sin∠ADB．

= ，∴sin∠CAD= sin∠ADC，

∵sin∠ADB=sin∠ADC，

∴ = ．

【解析】（1）△ABD中，由正弦定理可得AD的长；（2）利用BD=2DC，△ACD的面积为 ，求出BD，DC，利用余弦定理求出AC，利用正弦定理可得结论．