题目内容
若直线y=kx-2与曲线x=
有两个交点,则k范围是( )
| y2+4 |
A、(-
| ||||
B、(-
| ||||
C、(1,
| ||||
D、(-∞,-
|
考点:直线与圆锥曲线的关系
专题:圆锥曲线中的最值与范围问题
分析:首先,直线过定点(0,-2),曲线表示一个焦点在x轴上且等轴双曲线的右支,然后,结合直线与双曲线的位置关系和渐近线等求解范围.
解答:
解:∵直线y=kx-2,
∴该直线过定点(0,-2),
由曲线x=
,得
x2-y2=4,(x≥2),
它的渐近线为y=±x,
联立方程组
,消去y,并整理,得
(1-k2)x2+4kx-8=0,
根据题意,得该方程有两个不等实根,故
,
解得,1<k<
,
故选:C.
∴该直线过定点(0,-2),
由曲线x=
| y2+4 |
x2-y2=4,(x≥2),
它的渐近线为y=±x,
联立方程组
|
(1-k2)x2+4kx-8=0,
根据题意,得该方程有两个不等实根,故
|
解得,1<k<
| 2 |
故选:C.
点评:本题重点考查了直线与双曲线的位置关系、直线方程、等轴双曲线、双曲线的简单几何性质等知识,属于中档题.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
计算
cosxdx的结果是( )
| ∫ |
-
|
| A、4 | B、2 | C、0 | D、π |
sin13°cos47°+cos13°sin47°=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
(理科)已知-3<a<2,3<b<4,则
的取值范围为( )
| a |
| b |
A、(-1,
| ||||
B、(-
| ||||
C、(-1,
| ||||
D、(-
|
某学校有教师150人,其中高级教师15人,中级教师45人,初级教师90人.现按职称分层抽样选出30名教师参加教工代表大会,则选出的高、中、初级教师的人数分别为( )
| A、3,9,18 |
| B、5,10,15 |
| C、3,10,17 |
| D、5,9,16 |
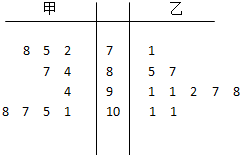 两名射击运动员甲、乙在某次比赛中的成绩(单位:环)用茎叶图表示如图,甲、乙两人射击成绩的中位数分别用n甲、n乙表示,则( )
两名射击运动员甲、乙在某次比赛中的成绩(单位:环)用茎叶图表示如图,甲、乙两人射击成绩的中位数分别用n甲、n乙表示,则( )| A、n甲>n乙 |
| B、n甲<n乙 |
| C、n甲=n乙 |
| D、n甲、n乙的大小关系不确定 |