题目内容
11.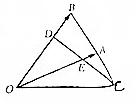 在△ABO中,点C是点B关于点A的对称点,点D是OB靠近B的三等分点,DC与OA交于E点,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OC}$,$\overrightarrow{CD}$.
在△ABO中,点C是点B关于点A的对称点,点D是OB靠近B的三等分点,DC与OA交于E点,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OC}$,$\overrightarrow{CD}$.
分析 根据平面向量加减运算的三角形法则即可用$\overrightarrow{a},\overrightarrow{b}$表示出$\overrightarrow{OC},CD$.
解答 解:∵C是点B关于点A的对称点,
∴$\overrightarrow{AC}$=$\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}=\overrightarrow{a}-\overrightarrow{b}$,
∴$\overrightarrow{OC}$=$\overrightarrow{OA}+\overrightarrow{AC}$=2$\overrightarrow{a}$-$\overrightarrow{b}$,
∵点D是OB靠近B的三等分点,
∴$\overrightarrow{BD}$=-$\frac{1}{3}$$\overrightarrow{OB}$=-$\frac{1}{3}$$\overrightarrow{b}$,
∴$\overrightarrow{CD}=\overrightarrow{CB}+\overrightarrow{BD}$=$-2\overrightarrow{AC}$+$\overrightarrow{BD}$=-2($\overrightarrow{a}-\overrightarrow{b}$)-$\frac{1}{3}\overrightarrow{b}$=-2$\overrightarrow{a}$+$\frac{5}{3}$$\overrightarrow{b}$.
点评 本题考查了平面向量的几何运算,属于基础题.

练习册系列答案
相关题目
1.已知某几何体的三视图如图所示,则该几何体的体积是( )
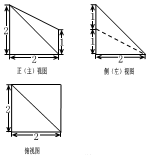

| A. | $\frac{2}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
19.某种电路开关闭合后会出现红灯或绿灯闪烁,已知开关第一次闭合后出现红灯的概率为$\frac{1}{2}$,两次闭合后都出现红灯的概率为$\frac{1}{5}$,则在第一次闭合后出现红灯的条件下第二次闭合后出现红灯的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{2}$ |
6.设集合A={y|y=$\sqrt{{x}^{2}-1}$},B={x|y=$\sqrt{{x}^{2}-1}$},则下列结论中正确的是( )
| A. | A=B | B. | A⊆B | C. | B⊆A | D. | A∩B={x|x≥1} |
3.已知抛物线C:y2=2px的焦点与圆x2+y2-2x-15=0的圆心重合,则抛物线C的方程是( )
| A. | y2=2x | B. | y2=-2x | C. | y2=4x | D. | y2=-4x |
1.执行如图所示的程序框图,如果输出T=6,那么判断框内应填入的条件是( )
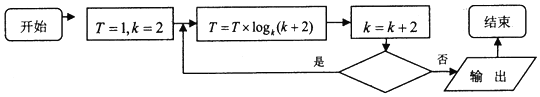
| A. | k<32 | B. | k<33 | C. | k<64 | D. | k<65 |