题目内容
已知各项都为正数的数列{an}的前行项和为Sn,且对任意n∈N*.都有2pSn=
+pan(其中p>0为常数),记数列{
}前通项的和为Hn.
(1)求数列{an}的通项公式及Hn;
(2)当p=2时,将数列{
}的前4项抽去其中一项后,剩下三项按原来顺序恰为等比数列{bn}的前3项,记{bn}的前n项和为Tn,若存在m∈N*,使对任意n∈N*.总有Tm<Hn+λ恒成立,求实数λ的取值范围.
| a | 2 n |
| 1 |
| Sn |
(1)求数列{an}的通项公式及Hn;
(2)当p=2时,将数列{
| 1 |
| an |
考点:数列与不等式的综合
专题:等差数列与等比数列
分析:(1)利用递推式及当n≥2时,an=Sn-Sn-1可得an-an-1=p>0,再利用等差数列的通项公式和前n项和公式可得an、Sn,再利用“裂项求和”可得Hn.
(2)当p=2时,an=2n,可得
=
,
=
,
=
,
=
,只有
,
,
成等比数列,利用等比数列的通项公式和前n项和公式可得bn、Tn.再利用Tm及Hn的单调性即可.
(2)当p=2时,an=2n,可得
| 1 |
| a1 |
| 1 |
| 2 |
| 1 |
| a2 |
| 1 |
| 4 |
| 1 |
| a3 |
| 1 |
| 6 |
| 1 |
| a4 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
解答:
解:(1)当n=1时,2pa1=
+pa1,∵a1>0,∴2p=a1+p,解得a1=p.
当n≥2时,由2pSn=
+pan,2pSn-1=
+pan-1,
可得2pan=
+pan-(
+pan-1),化为(an+an-1)(an-an-1-p)=0,
∵?n∈N*,都有an>0,
∴an-an-1=p>0,
∴数列{an}是等差数列,
∴an=p+(n-1)p=np.
∴Sn=
=
,
∴
=
(
-
).
∴Hn=
+
+…+
=
[(1-
)+(
-
)+…+(
-
)]
=
(1-
)=
•
.
(2)当p=2时,an=2n,∴
=
,
=
,
=
,
=
,
只有
,
,
成等比数列,∴数列{bn}的首项b1=
,公比q=
,∴bn=
•(
)n-1=(
)n.
Tn=
=1-(
)n.
∵Tm=1-(
)m是关于m的单调递增数列,∴
≤Tm<1.
又Hn=
•
=
的最小值为
.
∵存在m∈N*,使对任意n∈N*,总有Tm<Hn+λ恒成立,∴λ>
-
=0.
| a | 2 1 |
当n≥2时,由2pSn=
| a | 2 n |
| a | 2 n-1 |
可得2pan=
| a | 2 n |
| a | 2 n-1 |
∵?n∈N*,都有an>0,
∴an-an-1=p>0,
∴数列{an}是等差数列,
∴an=p+(n-1)p=np.
∴Sn=
| n2p2+np2 |
| 2p |
| (n2+n)p |
| 2 |
∴
| 1 |
| Sn |
| 2 |
| p |
| 1 |
| n |
| 1 |
| n+1 |
∴Hn=
| 1 |
| S1 |
| 1 |
| S2 |
| 1 |
| Sn |
| 2 |
| p |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 2 |
| p |
| 1 |
| n+1 |
| 2 |
| p |
| n |
| n+1 |
(2)当p=2时,an=2n,∴
| 1 |
| a1 |
| 1 |
| 2 |
| 1 |
| a2 |
| 1 |
| 4 |
| 1 |
| a3 |
| 1 |
| 6 |
| 1 |
| a4 |
| 1 |
| 8 |
只有
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
Tn=
| ||||
1-
|
| 1 |
| 2 |
∵Tm=1-(
| 1 |
| 2 |
| 1 |
| 2 |
又Hn=
| 2 |
| 2 |
| n |
| n+1 |
| n |
| n+1 |
| 1 |
| 2 |
∵存在m∈N*,使对任意n∈N*,总有Tm<Hn+λ恒成立,∴λ>
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题综合考查了等差数列与等比数列的通项公式和前n项和公式、“裂项求和”、数列的单调性等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
设a,b,c,d∈R,则“a>b,c>d”是“ac>bd”成立的 ( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
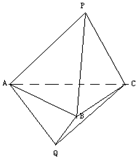 如图,在六面体PABCQ中,QA=QB=QC=AB=CB=CA=
如图,在六面体PABCQ中,QA=QB=QC=AB=CB=CA=