题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .过点
.过点![]() 做四棱锥
做四棱锥![]() 的截面
的截面![]() ,分别交
,分别交![]() ,
,![]() ,
,![]() 于点
于点![]() ,已知
,已知![]() ,
,![]() 为
为![]() 的中点.
的中点.

(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)在![]() 上取点
上取点![]() ,且满足
,且满足![]() ,连接
,连接![]() ,
,![]() ,可证
,可证![]() 是平行四边形,即可证明结论;
是平行四边形,即可证明结论;
(Ⅱ)建立空间直角坐标系,求平面![]() 的法向量,利用线面角公式计算即可求解.
的法向量,利用线面角公式计算即可求解.
(Ⅰ)证明:在![]() 上取点
上取点![]() ,且满足
,且满足![]() ,
,
连接![]() ,
,![]() ,则
,则![]() ,且
,且![]() ,
,
因为![]() ,
,
所以![]() ,且
,且![]()
所以![]() 是平行四边形,
是平行四边形,
所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ;
;
(Ⅱ)过点![]() 作与
作与![]() 平行的射线
平行的射线![]() ,易证两两垂直,
,易证两两垂直,
所以以![]() 为
为![]() 轴,以
轴,以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,如图,
,如图,

则有![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
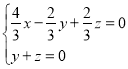 ,令
,令![]() ,解得
,解得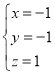
所以![]() 是平面
是平面![]() 的一个法向量
的一个法向量
因为点![]() 在
在![]() 上,所以
上,所以![]()
因为![]() 平面
平面![]() ,所以
,所以![]() ,
,
解得![]() ,所以
,所以![]()
或如下证法:因为![]() 平面
平面![]() 且平面
且平面![]() 平面
平面![]() ,
,
所以![]() ,
,
所以![]() ,
,
因为![]() 为
为![]() 中点,所以
中点,所以![]() 为
为![]() 中点,所以
中点,所以![]() ,
,
所以![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则
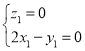 ,令
,令![]() ,解得
,解得
所以![]() 是平面
是平面![]() 的一个法向量,
的一个法向量,![]() ,
,
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目





