题目内容
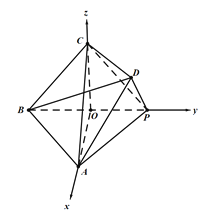
【题目】在四棱锥![]() 中,四边形
中,四边形![]() 是边长为2的菱形,
是边长为2的菱形,![]() 为正三角形,
为正三角形,![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,平面
,平面![]() 平面
平面![]() .
.
(1)求证:![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)由题意过![]() 作
作![]() ,
,![]() 为垂足,连接
为垂足,连接![]() ,可得到
,可得到![]() 平面
平面![]() ,根据
,根据![]() 与平面
与平面![]() 所成的角为
所成的角为![]() 即
即![]() ,根据边角关系可得到
,根据边角关系可得到![]() ,从而有
,从而有![]() 平面
平面![]() ,再根据四边形
,再根据四边形![]() 是边长为2的菱形可得
是边长为2的菱形可得![]() ,所以有
,所以有![]() 平面
平面![]() ,即可证明
,即可证明![]() ;
;
(2) 以![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 的方向分别为
的方向分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向.建立空间直角坐标系
轴的正方向.建立空间直角坐标系![]() ,写出相关点的坐标,求出平面
,写出相关点的坐标,求出平面![]() 与平面
与平面![]() 的法向量,利用数量积求夹角即可.
的法向量,利用数量积求夹角即可.
证明,(1)过![]() 作
作![]() ,
,![]() 为垂足,连接
为垂足,连接![]() .
.
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() .
.
所以![]() 平面
平面![]() ,
,
所以![]() 为
为![]() 与平面
与平面![]() 所成的角,即
所成的角,即![]() .
.
因为![]() .所以
.所以![]() ,
,
又![]() ,所以
,所以![]() 是
是![]() 的中点.
的中点.
因为![]() 为正三角形.所以
为正三角形.所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() .
.
因为四边形![]() 是边长为2的菱形,所以
是边长为2的菱形,所以![]() .
.
又![]() .所以
.所以![]() 平面
平面![]() .
.
所以![]() .
.
解:(2)以![]() 为原点,以
为原点,以![]() ,
,![]() ,
,![]() 的方向
的方向
分别为![]() 轴,
轴,![]() 轴,
轴,![]() 轴的正方向.建立空间直角坐标系
轴的正方向.建立空间直角坐标系![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,则
,则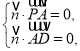 ,即
,即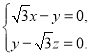
取![]() ,则
,则![]() ,
,
根据(1),![]() 平面
平面![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,则
,则
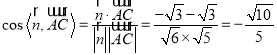 .
.
故平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

练习册系列答案
相关题目
【题目】疫情期间,为了更好地了解学生线上学习的情况,某兴趣小组在网上随机抽取了100名学生对其线上学习满意情况进行调查,其中男女比例为2∶3,其中男生有24人满意,女生有12人不满意.
(1)完成![]() 列联表,并回答是否有95%把握认为“线上学习是否满意与性别有关”
列联表,并回答是否有95%把握认为“线上学习是否满意与性别有关”
满意 | 不满意 | 合计 | |
男生 | |||
女生 | |||
合计 |
(2)从对线上学习满意的学生中,利用分层抽样抽取6名学生,再在6名学生中抽取3名,记抽到的女生人数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式:附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| .072 | 2.706 | 3.842 | 5.024 | 6.635 | 7.879 | 10.828 |






