题目内容
三棱锥P‐ABC的四个顶点均在同一球面内，其中△ABC是正三角形，PA⊥平面ABC，PA=2AB=6，则该球的体积是 ．
考点：球的体积和表面积
专题：空间位置关系与距离
分析：根据已知结合棱锥的几何特征和球的几何特征，求出球的半径，代入可得球的体积．
解答：
解：由已知PA⊥平面ABC，PA=2AB=6，△ABC是正三角形，
故平面ABC截球所得圆的半径r=
AB=
，
球心到平面ABC距离d=
PA=3，
故球的半径R=
=2
，
故球的体积V=
πR3=32
π；
故答案为：32
π
故平面ABC截球所得圆的半径r=
| ||
| 3 |
| 3 |
球心到平面ABC距离d=
| 1 |
| 2 |
故球的半径R=
| d2+r2 |
| 3 |
故球的体积V=
| 4 |
| 3 |
| 3 |
故答案为：32
| 3 |
点评：本题考查的知识点是球的体积，其中根据已知求出半径是解答的关键．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
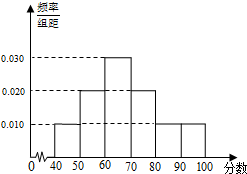某高校从参加今年自主招生考试的1000名学生中随机抽取100名学生的成绩进行统计，得到如图所示的样本频率分布直方图．若规定60分及以上为合格，则估计这1000名学生中合格人数是已知a=2ln3，b=2lg2，c=（
） log
，则（ ）
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、c＞a＞b |
| B、a＞b＞c |
| C、a＞c＞b |
| D、b＞c＞a |
复数z=
（i为虚数单位）在复平面内对应点的坐标是（ ）
| 2+4i |
| 1-i |
| A、（3，3） |
| B、（-1，3） |
| C、（3，-1） |
| D、（2，4） |