题目内容
16．一只蚂蚁在边长分别为6cm、8cm、10cm的三角形的边上爬行，该蚂蚁距离三角形的某个顶点的距离不超过1cm的概率为$\frac{1}{4}$．分析 本题考查的知识点是几何概型的意义，关键是要找出蚂蚁距离三角形的三个顶点的距离不超过1时对应线段的长度，并将它同三角形的周长代入几何概型的计算公式，进行求解．
解答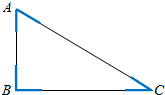 
解：如下图所示，当蚂蚁位于图中蓝色线段上时，距离三角形的三个顶点的距离不超过1，
由已知易得：蓝色线段的长度和为：6
三角形的周长为：6+8+10=24，
故P=$\frac{6}{24}$=$\frac{1}{4}$
故答案为：$\frac{1}{4}$
点评 几何概型的概率估算公式中的“几何度量”，可以为线段长度、面积、体积等，而且这个“几何度量”只与“大小”有关，而与形状和位置无关．解决的步骤均为：求出满足条件A的基本事件对应的“几何度量”N（A），再求出总的基本事件对应的“几何度量”N，最后根据P=$\frac{N（A）}{N}$求解．
练习册系列答案
相关题目
11．在四棱锥P-ABCD中，平面PAD⊥平面ABCD，△PAD为正三角形，底面ABCD为边长为2的正方形，点E为棱PB的中点，则点P到平面ACE的距离为（ ）
| A． | $\frac{\sqrt{7}}{7}$ | B． | $\frac{\sqrt{21}}{7}$ | C． | $\frac{\sqrt{35}}{7}$ | D． | $\frac{2\sqrt{21}}{7}$ |
1．为了宣传2015年10月在贵阳举行的“世界众筹大会”，“世界众筹大会”筹委会举办了“大众创业、万众创新”知识有奖问答活动，随机对市民15～65岁的人群抽样n人，回答问题统计结果如图所示：
（1）分别求出a，x的值；
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖，各组抽取的人数分别是多少？
（3）请根据频率分布直方图，估计样本数据的众数和中位数．
| 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 | 频率分布直方图 |
| 第1组 | [15，25） | 5 | 0.5 |  |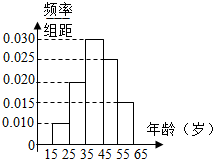
| 第2组 | [25，35） | a | 0.9 | |
| 第3组 | [35，45） | 27 | x | |
| 第4组 | [45，55） | 9 | 0.36 | |
| 第5组 | [55，65] | 3 | 0.2 |
（2）从第2，3，4组回答正确的人中用分层抽样的方法抽取6人，“世界众筹大会”筹委会决定给所抽取的6人颁发幸运奖，各组抽取的人数分别是多少？
（3）请根据频率分布直方图，估计样本数据的众数和中位数．
5．若点A（2，-4），点B（-2，-5），则向量$\overrightarrow{AB}$的坐标为（ ）
| A． | （-4，-1） | B． | （4，1） | C． | （0，-9） | D． | （-2，-5） |
8．已知$\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{AC}$，且$\overrightarrow{AC}=\overrightarrow a$，$\overrightarrow{BD}=\overrightarrow b$，则$\overrightarrow{AB}$=（ ）
| A． | $\frac{1}{2}（\overrightarrow a-\overrightarrow b）$ | B． | $\frac{1}{2}（\overrightarrow a+\overrightarrow b）$ | C． | $\frac{1}{2}（\overrightarrow b-\overrightarrow a）$ | D． | $\frac{1}{2}\overrightarrow a-\overrightarrow b$ |