题目内容
13.已知函数f(x)=$\frac{x+a}{{x}^{2}+bx+1}$是定义在R上的奇函数;(1)求a、b的值,判断并证明函数y=f(x)在区间(1,+∞)上的单调性
(2)已知k<0且不等式f(t2-2t+3)+f(k-1)<0对任意的t∈R恒成立,求实数k的取值范围.
分析 (1)由定义f(-x)=$\frac{-x+a}{{x}^{2}-bx+1}$=-$\frac{x+a}{{x}^{2}+bx+1}$,从而求出a=b=0,f(x)=$\frac{x}{{x}^{2}+1}$,利用导数性质能证明y=f(x)在区间(1,+∞)上的单调递减.
(2)由f(t2-2t+3)+f(k-1)<0及f(x)为奇函数得:f(t2-2t+3)<f(1-k),从而t2-2t+3>1-k任意的t∈R恒成立,由此能求出实数k的取值范围.
解答 解:(1)∵函数f(x)=$\frac{x+a}{{x}^{2}+bx+1}$是奇函数
∴由定义f(-x)=$\frac{-x+a}{{x}^{2}-bx+1}$=-$\frac{x+a}{{x}^{2}+bx+1}$,
∴a=b=0,
∴f(x)=$\frac{x}{{x}^{2}+1}$,
y=f(x)在区间(1,+∞)上的单调递减.
证明如下:
∵f(x)=$\frac{x}{{x}^{2}+1}$,∴${f}^{'}(x)=\frac{-{x}^{2}+1}{({x}^{2}+1)^{2}}$,
∵x>1,∴f′(x)<0,
∴y=f(x)在区间(1,+∞)上的单调递减.
(2)由f(t2-2t+3)+f(k-1)<0及f(x)为奇函数得:f(t2-2t+3)<f(1-k)
因为t2-2t+3≥2,1-k>1,且y=f(x)在区间(1,+∞)上的单调递减,
所以t2-2t+3>1-k任意的t∈R恒成立,
因为t2-2t+3的最小值为2,所以2>1-k,∴k>-1
∵k<0,∴-1<k<0.
∴实数k的取值范围是(-1,0).
点评 本题考查实数值的求法,考查函数的单调性的判断与证明,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.

 导学教程高中新课标系列答案
导学教程高中新课标系列答案| A. | 16π | B. | 12π | C. | 8π | D. | 4π |
| A. | {0} | B. | {1} | C. | {0,1} | D. | {0,-1} |
| A. | 6π | B. | $\sqrt{6}π$ | C. | 12π | D. | $2\sqrt{6}π$ |
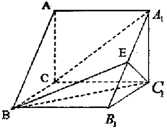 如图,三棱柱ABC-A1B1C1中,A1C1⊥BB1,AC=BC=BB1,E为A1B1的中点,且C1E⊥BB1.
如图,三棱柱ABC-A1B1C1中,A1C1⊥BB1,AC=BC=BB1,E为A1B1的中点,且C1E⊥BB1.