题目内容
2.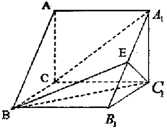 如图,三棱柱ABC-A1B1C1中,A1C1⊥BB1,AC=BC=BB1,E为A1B1的中点,且C1E⊥BB1.
如图,三棱柱ABC-A1B1C1中,A1C1⊥BB1,AC=BC=BB1,E为A1B1的中点,且C1E⊥BB1.(1)求证:A1C∥平面BEC1;
(2)求A1C与平面ABB1A所成角的大小.
分析 (1)连结B1C,交BC1于F,连结EF,推导出EF∥A1C,由此能证明A1C∥平面BEC1.
(2)取AB中点D,连结DE,DA1,DC,推导出C1E∥CD,CD⊥平面ABB1A1,∠CA1D是A1C与平面ABB1A所成角,由此能求出A1C与平面ABB1A所成角的大小.
解答 (本小题12分)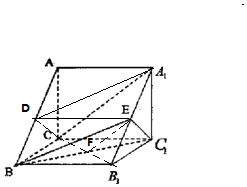
证明:(1)连结B1C,交BC1于F,连结EF,
∵三棱柱ABC-A1B1C1中,BB1C1C是平行四边形,∴F为B1C中点,
∵E为A1B1的中点,∴EF∥A1C,
∵EF?平面BEC1,A1C?平面BEC1,
∴A1C∥平面BEC1.…(4分)
解:(2)取AB中点D,连结DE,DA1,DC,
∵E为A1B1中点,∴三棱柱ABC-A1B1C1中,DE∥CC1,
∴四边形C1EDC是平行四边形,∴C1E∥CD,
∵C1E⊥A1B1,C1E⊥BB1,∴C1E⊥平面ABB1A1,
∴CD⊥平面ABB1A1,
∴∠CA1D是A1C与平面ABB1A所成角,
∵CD=$\frac{\sqrt{2}}{2}$AC,A1C=$\sqrt{2}AC$,
∴sin∠CA1D=$\frac{CD}{{A}_{1}C}$=$\frac{1}{2}$,∴$∠C{A}_{1}D=\frac{π}{6}$.
∴A1C与平面ABB1A所成角的大小为$\frac{π}{6}$.
点评 本题考查线面平行的证明,考查线面角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
12.双曲线$\frac{{x}^{2}}{16}-\frac{{y}^{2}}{9}$=1的渐近线方程为( )
| A. | y=±$\frac{16}{9}x$ | B. | y=±$\frac{9}{16}$x | C. | y=±$\frac{3}{4}$x | D. | y=±$\frac{4}{3}$x |
10.(1)设f(x)=ax+b,且$\int_{\;-1}^{\;1}{{{[{f(x)}]}^2}dx}=2$,求f(a)的取值范围.
(2)求函数f(x)=x3-3x过点P(1,-2)的切线方程.
(2)求函数f(x)=x3-3x过点P(1,-2)的切线方程.
17.已知实数x,y满足不等式组$\left\{\begin{array}{l}{x+2y+2≥0}\\{2x-y+2≤0}\\{x≤0}\end{array}\right.$,则z=3x-y的最大值为( )
| A. | 1 | B. | -$\frac{16}{5}$ | C. | -2 | D. | 不存在 |
13.已知A(-4,3)、B(2,5)、C(6,3)、D(-3,0),则直线AB与直线CD( )
| A. | 平行 | B. | 相交 | C. | 垂直 | D. | 以上都有可能 |
14.设y=e3,则y′等于( )
| A. | 3e2 | B. | e2 | C. | 0 | D. | e3 |