题目内容
已知向量 =(3sin α,cos α),
=(3sin α,cos α), =(2sin α,5sin α-4cos α),α∈
=(2sin α,5sin α-4cos α),α∈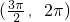 ,且
,且 .
.
(1)求tan α的值;
(2)求cos 的值.
的值.
解:(1)∵ ,∴
,∴ =0.
=0.
而 =(3sinα,cosα),
=(3sinα,cosα), =(2sinα,5sinα-4cosα),
=(2sinα,5sinα-4cosα),
故 =6sin2α+5sinαcosα-4cos2α=0.
=6sin2α+5sinαcosα-4cos2α=0.
由于cosα≠0,∴6tan2α+5tanα-4=0.
解之,得tanα=- ,或tanα=
,或tanα= .
.
∵α∈( ),tanα<0,
),tanα<0,
故tanα= (舍去).
(舍去).
∴tanα=- .
.
(2)∵
由tanα=- ,求得tan
,求得tan =-
=- 或tan
或tan =2(舍去)
=2(舍去)
∴sin ,cos
,cos
cos( )=cos
)=cos cos
cos -sin
-sin sin
sin
= =-
=-
分析:( 1)通过向量关系,求 =0,化简后,求出tanα=-
=0,化简后,求出tanα=- .
.
(2)根据α的范围,求出 的范围,确定
的范围,确定 的正弦、余弦的值,利用两角和的余弦公式求出cos
的正弦、余弦的值,利用两角和的余弦公式求出cos 的值.
的值.
点评:本题考查两角和与差的余弦函数,数量积的坐标表达式,弦切互化,考查计算能力,是基础题.
 ,∴
,∴ =0.
=0.而
 =(3sinα,cosα),
=(3sinα,cosα), =(2sinα,5sinα-4cosα),
=(2sinα,5sinα-4cosα),故
 =6sin2α+5sinαcosα-4cos2α=0.
=6sin2α+5sinαcosα-4cos2α=0.由于cosα≠0,∴6tan2α+5tanα-4=0.
解之,得tanα=-
 ,或tanα=
,或tanα= .
.∵α∈(
 ),tanα<0,
),tanα<0,故tanα=
 (舍去).
(舍去).∴tanα=-
 .
.(2)∵

由tanα=-
 ,求得tan
,求得tan =-
=- 或tan
或tan =2(舍去)
=2(舍去)∴sin
 ,cos
,cos
cos(
 )=cos
)=cos cos
cos -sin
-sin sin
sin
=
 =-
=-
分析:( 1)通过向量关系,求
 =0,化简后,求出tanα=-
=0,化简后,求出tanα=- .
.(2)根据α的范围,求出
 的范围,确定
的范围,确定 的正弦、余弦的值,利用两角和的余弦公式求出cos
的正弦、余弦的值,利用两角和的余弦公式求出cos 的值.
的值.点评:本题考查两角和与差的余弦函数,数量积的坐标表达式,弦切互化,考查计算能力,是基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目