题目内容
13.已知圆C的圆心极坐标为(2,$\frac{π}{4}$),半径为1.(1)求圆C的极坐标方程;
(2)若Q是圆C上动点,点P在直线OQ上,且$\overrightarrow{OP}$=2$\overrightarrow{OQ}$,求点P轨迹的极坐标方程.
分析 (1)先求出圆的直角坐标方程,再由ρ2=x2+y2,ρcosθ=x,θ=y,能求出圆C的极坐标方程.
(2)设Q($\sqrt{2}+cosθ$,$\sqrt{2}+sinθ$),(0≤θ<2π)P(x,y),由$\overrightarrow{OP}$=2$\overrightarrow{OQ}$,得(x,y)=(2$\sqrt{2}+2cosθ$,2$\sqrt{2}+2sinθ$),由此先求出P的直角坐标方程,再由ρ2=x2+y2,ρcosθ=x,θ=y,能求出点P轨迹的极坐标方程.
解答 解:(1)∵圆C的圆心极坐标为(2,$\frac{π}{4}$),半径为1.
∴x=2cos$\frac{π}{4}$=$\sqrt{2}$,y=2sin$\frac{π}{4}$=$\sqrt{2}$,
∴圆的直角坐标方程为(x-$\sqrt{2}$)2+(y-$\sqrt{2}$)2=1,
即${x}^{2}+{y}^{2}-2\sqrt{2}x-2\sqrt{2}y+3=0$,
由ρ2=x2+y2,ρcosθ=x,θ=y,
得圆C的极坐标方程为${ρ}^{2}-2\sqrt{2}ρ(cosθ+sinθ)+3$=0.
(2)∵Q是圆C上动点,O( ),0),∴设Q($\sqrt{2}+cosθ$,$\sqrt{2}+sinθ$),(0≤θ<2π)
设P(x,y),∵$\overrightarrow{OP}$=2$\overrightarrow{OQ}$,∴(x,y)=(2$\sqrt{2}+2cosθ$,2$\sqrt{2}+2sinθ$),
∴$\left\{\begin{array}{l}{x=2\sqrt{2}+2cosθ}\\{y=2\sqrt{2}+2sinθ}\end{array}\right.,0≤θ<2π$,
∴P的直角坐标方程为$(x-2\sqrt{2})^{2}+(y-2\sqrt{2})^{2}=4$,
即${x}^{2}+{y}^{2}-4\sqrt{2}x-4\sqrt{2}y+12=0$,
由ρ2=x2+y2,ρcosθ=x,θ=y,
得点P轨迹的极坐标方程为${ρ}^{2}-4\sqrt{2}ρ(cosθ+sinθ)+12=0$.
点评 本题考查圆的极坐标方程和点的轨迹的极坐标方程的求法,是中档题,解题时要认真审题,注意直角坐标方程和极坐标方程转化公式的合理运用.

 阅读快车系列答案
阅读快车系列答案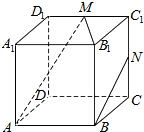 如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:
如图,在正方体ABCD-A1B1C1D1中,M、N分别为棱C1D1、C1C的中点,有以下四个结论:①直线AM与CC1是相交直线;
②直线AM与BN是平行直线;
③直线BN与MB1是异面直线;
④直线AM与DD1是异面直线.
其中正确的结论为( )
| A. | ③④ | B. | ①② | C. | ①③ | D. | ②④ |
| A. | d(∫f(x)dx)=f(x)dx | B. | ∫f(x)dx=∫f(u)du | ||
| C. | ${∫}_{a}^{b}$f(x)dx=${∫}_{a}^{b}$f(u)du | D. | ${∫}_{a}^{b}$f(x)dx+${∫}_{b}^{a}$f(x)dx=0. |