题目内容
10.在△ABC中,角A,B,C的对边分别为a,b,c,已知a-c=$\frac{\sqrt{3}}{3}$bsinA-bcosA(Ⅰ)求B;
(Ⅱ)若b=$\sqrt{3}$,△ABC的面积S=$\frac{\sqrt{3}}{2}$,求△ABC的周长.
分析 (I)利用正弦定理将边化弦,利用三角函数的恒等变换化简得出B的三角函数值;
(II)根据面积公式得出ac,利用余弦定理解得a+c,从而得出三角形的周长.
解答 解:(I)∵a-c=$\frac{\sqrt{3}}{3}$bsinA-bcosA,∴sinA-sinC=$\frac{\sqrt{3}}{3}$sinBsinA-sinBcosA,
∵sinC=sin(A+B)=sinAcosB+cosAsinB,
∴sinA-sinAcosB=$\frac{\sqrt{3}}{3}$sinBsinA,
∵sinA≠0,
∴1-cosB=$\frac{\sqrt{3}}{3}$sinB.即cosB=1-$\frac{\sqrt{3}}{3}$sinB.
又sin2B+cos2B=1,
∴sinB=$\frac{\sqrt{3}}{2}$,cosB=$\frac{1}{2}$.
∴B=$\frac{π}{3}$.
(II)∵S△ABC=$\frac{1}{2}acsinB$=$\frac{\sqrt{3}}{4}ac$=$\frac{\sqrt{3}}{2}$,
∴ac=2.
由余弦定理得cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{(a+c)^{2}-2ac-{b}^{2}}{2ac}$=$\frac{(a+c)^{2}-7}{4}=\frac{1}{2}$,
∴a+c=3.
∴a+b+c=3+$\sqrt{3}$.
点评 本题考查了正弦定理,余弦定理,三角形的面积公式,属于中档题.

练习册系列答案
相关题目
2.如图所示,双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1,F2,M,N为双曲线C上两点,且kMN=0,若$\overrightarrow{{F}_{1}Q}$=$\overrightarrow{QN}$(Q在双曲线C上),且|MN|=$\frac{{|F}_{1}{F}_{2}|}{4}$,则双曲线C的渐近线方程为( )
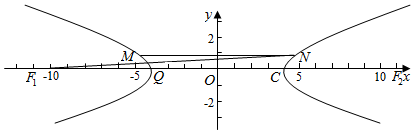
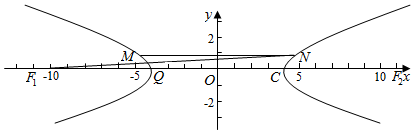
| A. | y=$±\sqrt{2}$x | B. | y=$±\sqrt{3}$x | C. | y=±2x | D. | y=$±\sqrt{5}$x |