题目内容
四边形ABCD是边长为10的正方形,以A点为圆心,9为半径画弧,分别交AB,AD于点E,F,P为EF上一动点,过P点分别作PM⊥BC,PN⊥CD,垂足为M,N,求矩形PMCN的面积的最小值.
考点:基本不等式在最值问题中的应用
专题:计算题,作图题,函数的性质及应用
分析:由题意建立平面直角坐标系并设点P(x,y),从而可得x+y=9,(0≤x≤9);从而表示出S矩形PMCN=PM•PN=(10-x)(10-y),化简求最值即可.
解答:
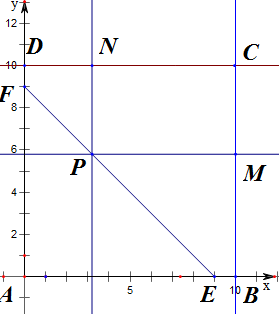 解:如图建立平面直角坐标系,设点P(x,y);
解:如图建立平面直角坐标系,设点P(x,y);
则x+y=9,(0≤x≤9);
S矩形PMCN=PM•PN=(10-x)(10-y)
=100-10(x+y)+xy
=10+xy
=10+x(9-x)
=-x2+9x+10;
故当x=0或x=9时,
S矩形PMCN有最小值10;
故矩形PMCN的面积的最小值为10.
 解:如图建立平面直角坐标系,设点P(x,y);
解:如图建立平面直角坐标系,设点P(x,y);则x+y=9,(0≤x≤9);
S矩形PMCN=PM•PN=(10-x)(10-y)
=100-10(x+y)+xy
=10+xy
=10+x(9-x)
=-x2+9x+10;
故当x=0或x=9时,
S矩形PMCN有最小值10;
故矩形PMCN的面积的最小值为10.
点评:本题考查了数形结合的思想应用及函数的性质应用,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
若曲线y=alnx+x2(a>0)的切线倾斜角的取值范围是[
,
),则a=( )
| π |
| 3 |
| π |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=2sin[π(x+1)]-
在x∈(
,3)时的零点在下列哪个区间上( )
| 1 |
| x-1 |
| 3 |
| 2 |
A、(
| ||||
B、(
| ||||
C、(2,
| ||||
D、(
|
已知 f(x)=x2-2x+8,如果g(x)=f(x+2),则g(x)( )
| A、在区间(-∞,1)上是单调减函数,在区间(1,+∞)上是单调增函数 |
| B、在区间(-∞,0)上是单调减函数,在区间(0,+∞)上是单调增函数 |
| C、在区间(-∞,-1)上是单调减函数,在区间(-1,+∞)上是单调增函数 |
| D、在区间(-∞,3]上是单调减函数,在区间[3,+∞)上是单调增函数 |
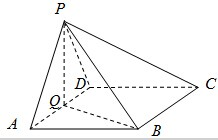 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,Q为AD的中点.