题目内容
圆锥轴截面的顶角是120°，过顶点的截面面积的最大值为8，则它的体积是（ ）
A、4
| ||
| B、8π | ||
C、8
| ||
| D、24π |
考点：旋转体（圆柱、圆锥、圆台）,棱柱、棱锥、棱台的体积
专题：计算题,空间位置关系与距离
分析：作图可知，r=
h，求最大面积时高的值，代入求体积．
| 3 |
解答：
解：则由右图知，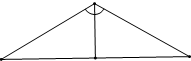
r=
h，
过顶点的截面为等腰三角形，
设底边长为2x，与圆心的距离为d，
则d2+x2=r2，
截面等腰三角形底边上的高为
；
则截面等腰三角形的面积为
S=
•2x•
=x•
=x•
=
≤
=2h2．
（当且仅当x2=4h2-x2，即x=
h时，等号成立．
则2h2=8，解得，h=2，则r=
h=2
．
则V=
•π•r2h=
•π•12•2=8π．
故选B．
r=| 3 |
过顶点的截面为等腰三角形，
设底边长为2x，与圆心的距离为d，
则d2+x2=r2，
截面等腰三角形底边上的高为
| d2+h2 |
则截面等腰三角形的面积为
S=
| 1 |
| 2 |
| d2+h2 |
=x•
| r2-x2+h2 |
=x•
| 4h2-x2 |
=
| x2(4h2-x2) |
≤
| x2+4h2-x2 |
| 2 |
（当且仅当x2=4h2-x2，即x=
| 2 |
则2h2=8，解得，h=2，则r=
| 3 |
| 3 |
则V=
| 1 |
| 3 |
| 1 |
| 3 |
故选B．
点评：本题考查了学生的空间想象力，及基本不等式．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
据统计，一名工人组装第x件某产品所用的时间（单位：分钟）f（x）=
（m，c为常数），已知工人组装第4件产品所用的时间为30分钟，工人组装第m件产品所用的时间为15分钟，则m=（ ）
|
| A、49 | B、25 | C、16 | D、9 |
已知函数y=
关于原点对称，则函数f（x）=
-1的对称中心的坐标为（ ）
| cosx |
| x |
2cos2(
| ||||
| x-1 |
| A、（-1，1） |
| B、（1，1） |
| C、（1，-1） |
| D、（-1，-1） |
若数列{an}满足：a1=19，an+1=an-2（n∈N+），则数列{an}的前n项和最大时，n的值是（ ）
| A、9 | B、10 | C、11 | D、12 |
若a=2x，b=log
x，则“a＞b”是“x＞1”的（ ）
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
下列各组函数中，表示同一个函数的是（ ）
A、f（x）=
| |||
B、f（x）=logaax（a＞0，a≠1），g（x）=
| |||
C、f（x）=x，g（x）=
| |||
| D、f（x）=lnx2，g（x）=2lnx |
若P、Q是两个非空数集，定义P与Q的差集P-Q={x|x∈P且x∉Q}，已知集合A={x|a＜x＜0}，集合B={x|-b＜x＜b}，其中a，b是满足|a|≥|b|的整数，在集合A中随机取一个整数c，若c属于差集A-B的概率P1=
，属于集合A∩B的概率P2=
，则整数a，b应满足的条件是（ ）
| 2 |
| 3 |
| 1 |
| 3 |
| A、a+3b=-1（b≥1，b∈Z） |
| B、a+3b=-1，（b≥2，b∈Z） |
| C、a+3b=2（b≥1，b∈Z） |
| D、a+3b=2，（b≥2，b∈Z） |
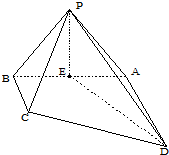如图，四棱锥P-ABCD中，底面ABCD是直角梯形，∠DAB=90°，AD∥BC，AD⊥侧面PAB，△PAB是等边三角形，DA=AB=2=0，BC=