题目内容
2.$\frac{2cos10°-sin20°}{sin70°}$=$\sqrt{3}$.分析 利用两角和差的余弦公式,进行化简即可.
解答 解:原式=$\frac{2cos(30°-20°)-sin20°}{cos20°}$=$\frac{2(\frac{\sqrt{3}}{2}cos20°+\frac{1}{2}sin20°)-sin20°}{cos20°}$
=$\frac{\sqrt{3}cos20°+sin20°-sin20°}{cos20°}$=$\frac{\sqrt{3}cos20°}{cos20°}$=$\sqrt{3}$,
故答案为:$\sqrt{3}$.
点评 本题主要考查三角函数值的化简,利用两角和差的余弦公式是解决本题的关键.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
12.在△ABC中,已知(a2+b2-c2)2=2(ab)2,则C等于( )
| A. | 30° | B. | 45° | C. | 60° | D. | 45°或135° |
17.在△ABC中,a,b,c分别是角A、B、C的对边,且sin2(${\frac{π-A}{2}}$)=$\frac{b+c}{2c}$,则△ABC的形状是( )
| A. | 直角三角形 | B. | 等腰三角形或直角三角形 | ||
| C. | 正三角形 | D. | 等腰直角三角形 |
12.直三棱柱ABC-A1B1C1中,∠B1BC1=30°,AB=BC=CA,M、N分别是棱AA1、A1B1中点,则MN与AC所成的角的余弦值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{1}{3}$ |
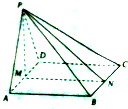 如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,平面PAD⊥平面ABCD,M和N分别是AD和BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,平面PAD⊥平面ABCD,M和N分别是AD和BC的中点. 在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$
在四棱锥P-ABCD中,PA⊥平面ABCD,△ABC是正三角形,AC与BD的交点M恰好是AC中点,又PA=AB=4,∠CDA=120°,点N在线段PB上,且PN=$\sqrt{2}$