题目内容
13.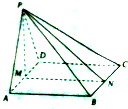 如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,平面PAD⊥平面ABCD,M和N分别是AD和BC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,△PAD是正三角形,平面PAD⊥平面ABCD,M和N分别是AD和BC的中点.(1)求证:PM⊥MN;
(2)求证:平面PMN⊥平面PBC;
(3)在PA上是否存在点Q,使得平面QMN∥平面PCD?若存在求出Q点位置,并证明;若不存在,请说明理由.
分析 (1)易证PM⊥AD,由平面PAD⊥平面ABCD,可证PM⊥平面ABCD,MN?平面ABCD,从而证明PM⊥MN;
(2)由(1)可得:PM⊥BC,又底面ABCD是正方形,M和N分别是AD和BC的中点,可证BC⊥MN,从而证明BC⊥平面PMN,即可证明平面PMN⊥平面PBC;
(3)取PA的中点Q,连接QM,QN,可证QM∥PD,又MN∥DC,从而证明平面QMN∥平面PCD.
解答  证明:(1)∵△PAD是正三角形,M是AD的中点.
证明:(1)∵△PAD是正三角形,M是AD的中点.
∴PM⊥AD,
∵平面PAD⊥平面ABCD,PM?平面PAD,平面PAD∩平面ABCD=AD,
∴PM⊥平面ABCD,MN?平面ABCD,
∴PM⊥MN;
(2)∵由(1)可得:PM⊥BC,
又∵底面ABCD是正方形,M和N分别是AD和BC的中点.
∴BC⊥MN,
∵PM∩MN=M,
∴BC⊥平面PMN,
∵BC?平面PBC,
∴平面PMN⊥平面PBC;
(3)当Q为PA的中点时,使得平面QMN∥平面PCD,
证明:如图,取PA的中点Q,连接QM,QN,
∵Q,M分别为PA,AD的中点,
∴△APD中,QM∥PD,
∵底面ABCD是正方形,M和N分别是AD和BC的中点.
∴MN∥DC,
又∵MN∩QM=M,CD∩PD=D,
∴平面QMN∥平面PCD.
点评 本题主要考查了平面与平面垂直的判定,平面与平面平行的判定,考查了空间想象能力和转化思想,属于中档题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
1.定义域为R的函数f(x)对任意x都有f(x)=f(4-x),且其导函数f′(x)满足(x-2)f′(x)>0,则当2<m<4时,有( )
| A. | f(2)>f(2m)>f(log2m) | B. | f(log2m)>f(2m)>f(2) | C. | f(2m)>f(log2m)>f(2) | D. | f(2m)>>f(2)>f(log2m) |
8.定义在R上的偶函数y=f(x)满足f(x+1)=-f(x),且当x∈(0,1]时单调递增,则( )
| A. | $f(\frac{1}{3})<f(-5)<f(\frac{5}{2})$ | B. | $f(\frac{1}{3})<f(\frac{5}{2})<f(-5)$ | C. | $f(\frac{5}{2})<f(\frac{1}{3})<f(-5)$ | D. | $f(-5)<f(\frac{1}{3})<f(\frac{5}{2})$ |
3.设三次函数f(x)=ax3+bx2+cx+1的导函数为f′(x)=3ax(x-2),若函数y=f(x)共有三个不同的零点,则a的取值范围是( )
| A. | (-∞,-$\frac{1}{4}$) | B. | (0,$\frac{1}{4}$) | C. | ($\frac{1}{4}$,+∞) | D. | (0,2) |