题目内容
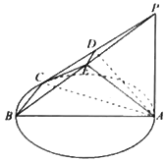
【题目】如图,点![]() 在以
在以![]() 为直径的上运动,
为直径的上运动,![]() 平面
平面![]() ,且
,且![]() ,点
,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)证明![]() 平面
平面![]() 可得
可得![]() ,再结合
,再结合![]() 即可得出
即可得出![]() 平面
平面![]() ,故而平面
,故而平面![]() 平面
平面![]() ;
;
(2)建立空间直角坐标系,求出两半平面的法向量,计算法向量的夹角即可得出二面角的大小.
(1)证明:∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() 是圆的直径,∴
是圆的直径,∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() .
.
∴![]() ,
,
∵![]() 是
是![]() 的中位线,∴
的中位线,∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)解:∵![]() 是圆的直径,∴
是圆的直径,∴![]() ,
,
∵![]() ,不妨设
,不妨设![]() ,则
,则![]() ,
,![]() ,
,
以![]() ,
,![]() 和平面
和平面![]() 过
过![]() 的垂线为坐标轴建立空间直角坐标系,如图所示,
的垂线为坐标轴建立空间直角坐标系,如图所示,

∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,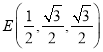 ,
,
∴![]() ,
, ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则 ,即
,即 ,
,
令![]() 得
得![]() ,
,
由(1)知![]() 平面
平面![]() ,故
,故![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
∴ .
.
∴平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
【题目】某市劳动部门坚持就业优先,釆取多项措施加快发展新兴产业,服务经济,带来大量就业岗位,据政府工作报告显示,截至2018年末,全市城镇新增就业21.9万人,创历史新高.城镇登记失业率为4.2%,比上年度下降0.73个百分点,处于近20年来的最低水平.
(1)现从该城镇适龄人群中抽取100人,得到如下列联表:
失业 | 就业 | 合计 | |
男 | 3 | 62 | 65 |
女 | 2 | 33 | 35 |
合计 | 5 | 95 | 100 |
根据联表判断是否有99%的把握认为失业与性别有关?
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |

(2)调查显示,新增就业人群中,新兴业态,民营经济,大型国企对就业支撑作用不断增强,其岗位比例为2∶5∶3,现要抽取一个样本容量为50的样本,则这三种岗位应该各抽取多少人?