Question

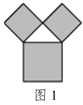
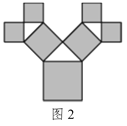
【题目】毕达哥拉斯树是由毕达哥拉斯根据“勾股定理”所画出来的一个可以无限重复的图形，也叫“勾股树”，其是由一个等腰直角三角形分别以它的每一条边向外作正方形而得到.图1所示是第1代“勾股树”，重复图1的作法，得到第2代“勾股树”(如图2)，如此继续.若“勾股树”上共得到8191个正方形，设初始正方形的边长为1，则最小正方形的边长为（ ）

A.B.C.D.

Answer 1

【答案】B

【解析】

由图可知，设第个图中正方形的个数为，则，结合累加法可求出，令，可确定第12个图形中得到8191个正方形；结合边长规律，即第个图中最小正方形边长为，从而可求出答案.

解：设第个图中正方形的个数为，则由图可知

则 ，将个式子相加可得 ，

所以，当时，，

所以.令，解得.

由题意知，第一个图中最小正方形边长为 ，第二个图中最小正方形边长为，

则第个图中最小正方形边长为，则.

故选:B.