题目内容
19.集合A={x|m•4x-(m+1)•2x+1=0}只有一个元素,求实数m的取值范围.分析 分类讨论m=0和m≠0两种情况进行讨论.
解答 解:当m=0时,2x=1,解得x=0;符号题意;
当m≠0时,令2x=t,(t>0)
∴原方程可化为:mt2-(m+1)t+1=0,(1)
原方程只有一个元素,故(1)只有一个正根,
∴△=(m+1)2-4m=0,或$\left\{\begin{array}{l}{△=(m+1)^{2}-4m>0}\\{\frac{1}{m}<0}\end{array}\right.$
解得:m=1;或m<0
综上,m≤0,或m=1.
点评 本题主要考查方程根的情况,属于中等题.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
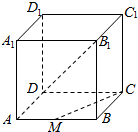
 如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,点M是AD的中点,点P是BM的中点,点Q在线段AC上,且AQ=3QC,取BD的中点O,以点O为原点,OD,OP所在直线为y,z轴,建立空间直角坐标系Oxyz
如图,在四面体A-BCD中,AD⊥平面BCD,BC⊥CD,AD=2,BD=2$\sqrt{2}$,点M是AD的中点,点P是BM的中点,点Q在线段AC上,且AQ=3QC,取BD的中点O,以点O为原点,OD,OP所在直线为y,z轴,建立空间直角坐标系Oxyz