题目内容
19．已知函数f（x）=$\left\{\begin{array}{l}{{3}^{x}，x≤1}\\{-x+4，x＞1}\end{array}\right.$；若f（x）=2，则x=2或log32．分析 利用函数的解析式，列出方程求解即可．
解答 解：函数f（x）=$\left\{\begin{array}{l}{{3}^{x}，x≤1}\\{-x+4，x＞1}\end{array}\right.$；
f（x）=2，
当x≤1时，3x=2，解得x=log32．
当x＞1时，-x+4=2，解得x=2，
故答案为：2或log32．
点评 本题考查分段函数的应用，函数的零点与方程根的关系，考查计算能力．
练习册系列答案
相关题目
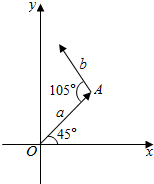在直角坐标系中，|$\overrightarrow{a}$|=4，|$\overrightarrow{b}$|=3，$\overrightarrow{a}$，$\overrightarrow{b}$如图所示，求它们的坐标．