题目内容
12.已知椭圆C:x2+4y2=4,直线$y=\frac{1}{2}x+b$与椭圆C交于不同的两点A,B.(Ⅰ)求椭圆C的焦点坐标;
(Ⅱ)求实数b的取值范围;
(Ⅲ)若b=1,求弦AB的长.
分析 (Ⅰ)将椭圆方程化为标准方程,求得a,b,c,即可得到所求焦点;
(Ⅱ)将直线方程代入椭圆方程,消去y,得到x的方程,再由判别式大于0,解不等式即可得到所求范围;
(Ⅲ)若b=1,设A(x1,y1),B(x2,y2),运用韦达定理和弦长公式,计算即可得到所求值.
解答 解:(Ⅰ)由椭圆方程x2+4y2=4得$\frac{x^2}{4}+{y^2}=1$,
可知 a2=4,b2=1,c2=3,
所以椭圆C的焦点坐标$(-\sqrt{3},0),(\sqrt{3},0)$;
(Ⅱ)直线方程与椭圆C的方程联立,得方程组$\left\{\begin{array}{l}y=\frac{1}{2}x+b\\{x^2}+4{y^2}=4\end{array}\right.$,
消y,整理得x2+2bx+2b2-2=0,①,
由直线l与椭圆C交于不同的两点A,B,则有△=4b2-4(2b2-2)>0,
解得$-\sqrt{2}<b<\sqrt{2}$;
(Ⅲ)若b=1,设A(x1,y1),B(x2,y2),
由(Ⅱ)中的①式得x1+x2=-2,x1x2=0,且k=$\frac{1}{2}$,
可得弦长$|AB|=\sqrt{(1+{k^2})[{{({x_1}+{x_2})}^2}-4{x_1}{x_2}]}=\sqrt{5}$.
点评 本题考查椭圆方程及运用,考查直线和椭圆方程联立,运用判别式大于0和韦达定理,以及弦长公式,考查运算能力,属于基础题.

练习册系列答案
相关题目
7.若方程${x^2}+\frac{y^2}{m}=4$表示焦点在x轴上的椭圆,则实数m的取值范围是( )
| A. | (0,1) | B. | (0,2) | C. | (1,2) | D. | (1,+∞) |
 如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E、F、H分别为AD、CD、DD1的中点,EF与BD交于点G.
如图,在四棱柱ABCD-A1B1C1D1中,AC⊥B1D,BB1⊥底面ABCD,E、F、H分别为AD、CD、DD1的中点,EF与BD交于点G.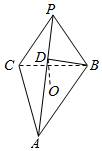 三棱锥P-ABC,底面是边长为2的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为PA上一点,AD=2DP,O为底面三角形中心.
三棱锥P-ABC,底面是边长为2的正三角形,平面PBC⊥平面ABC,PB=PC=2,D为PA上一点,AD=2DP,O为底面三角形中心. 如图,AB是⊙O的直径,点P是⊙O圆周上异于A,B的一点,AD⊥⊙O所在的平面PAB,四边形ABCD是边长为2的正方形,连结PA,PB,PC,PD.
如图,AB是⊙O的直径,点P是⊙O圆周上异于A,B的一点,AD⊥⊙O所在的平面PAB,四边形ABCD是边长为2的正方形,连结PA,PB,PC,PD.