题目内容
4.已知$\overrightarrow{OA}$=(3,2),$\overrightarrow{OB}$=(-4,y)并且$\overrightarrow{OB}$⊥$\overrightarrow{OA}$,则|$\overrightarrow{OB}$|=2$\sqrt{13}$.分析 通过向量的垂直关系求出y,然后求解向量的模.
解答 解:$\overrightarrow{OA}$=(3,2),$\overrightarrow{OB}$=(-4,y)并且$\overrightarrow{OB}$⊥$\overrightarrow{OA}$,
可得-12+2y=0,解得y=6,
$\overrightarrow{OB}$=(-4,6).
|$\overrightarrow{OB}$|=$\sqrt{16+36}$=$\sqrt{52}$=2$\sqrt{13}$.
故答案为:2$\sqrt{13}$.
点评 本题考查向量的垂直条件的应用,向量的模的求法,考查计算能力.

练习册系列答案
相关题目
12.已知P=log45,Q=log54,R=log4(log54),则( )
| A. | R<Q<P | B. | P<R<Q | C. | Q<R<P | D. | R<P<Q |
16.已知平行线3x+2y-6=0和6x+4y-3=0,则与这两条平行线距离相等的点的轨迹是( )
| A. | 3x+2y-4=0 | B. | 3x+2y-5=0 | C. | 6x+4y-9=0 | D. | 12x+8y-15=0 |
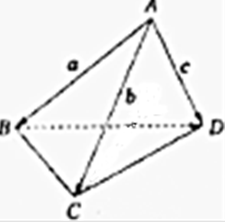 已知A、B、C、D是空间四个不同的点,求证:AC⊥BD的等价条件是AD2+BC2=CD2+AB2.
已知A、B、C、D是空间四个不同的点,求证:AC⊥BD的等价条件是AD2+BC2=CD2+AB2.