题目内容
13.火车站有某公司待运的甲种货物1530t,乙种货物1150t,现计划用A、B两种型号的车厢共50节运送这批货物,已知35t甲种货物和15t乙种货物可装满一节A型贷厢;25t甲种贷物和35t乙种货物可装满一节B型货厢,据此安排A、B两种货厢的节数,共有几种方案?若每节A型货厢的运费是0.5万元,每节B型货厢的运费是0.8万元,哪种方案的运费最少?分析 设安排A、B两种货厢x节,y节;从而得到约束条件$\left\{\begin{array}{l}{35x+25y≥1530}\\{15x+35y≥1150}\\{x+y≤50}\\{x≥0}\\{y≥0}\end{array}\right.$,从而作平面区域,利用数形结合求解即可.
解答 解:设安排A、B两种货厢x节,y节;
则$\left\{\begin{array}{l}{35x+25y≥1530}\\{15x+35y≥1150}\\{x+y≤50}\\{x≥0}\\{y≥0}\end{array}\right.$,
作平面区域如下,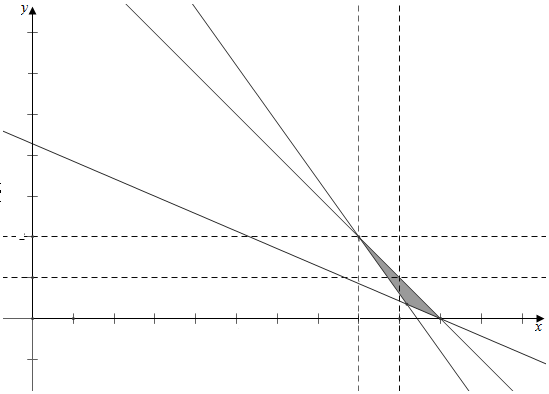 ,
,
结合图象可得,
有三种方案,分别为:
安排A、B两种货厢28节,22节,
安排A、B两种货厢29节,21节,
安排A、B两种货厢30节,20节;
易知执行第三种方案,即安排A、B两种货厢30节,20节时,
费用最少,为30×0.5+20×0.8=31万元.
点评 本题考查了线性规划在实际问题中的应用,同时考查了数形结合的思想应用.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
1.已知直线l1:x+ay-1=0,直线l2:ax+(a-2)y+3=0,其中a∈R,则“a=1”是“l1⊥l2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
5.在△ABC中M是BC的中点,BC=8,AM=3,AM⊥BC,则$\overrightarrow{AB}$•$\overrightarrow{AC}$=( )
| A. | -7 | B. | -$\frac{7}{2}$ | C. | 0 | D. | 7 |
2.函数f(x)=sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的最小正周期为π,且其图象经过点($\frac{7π}{12}$,0),则函数f(x)在区间[0,$\frac{π}{2}$]上的最大值与最小值的和为( )
| A. | 1-$\frac{\sqrt{3}}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | 1+$\frac{\sqrt{3}}{2}$ |