题目内容
14.在三棱锥A1-ABC中,AA1⊥底面ABC,BC⊥A1B,AA1=AC=2,则该三棱锥的外接球的表面积为8π.分析 将三棱锥补成长方体,它的对角线是其外接球的直径,从而即可求得该三棱锥的外接球的表面积.
解答 解:由三棱锥A1-ABC中,AA1⊥底面ABC,BC⊥A1B,将三棱锥补成长方体,它的对角线是其外接球的直径,则
三棱锥外接球的直径为2$\sqrt{2}$,半径为$\sqrt{2}$,
∴外接球的表面积S=4πR2=8π.
故答案为:8π.
点评 本题考查球的表面积的计算,考查学生分析解决问题的能力,得出将三棱锥补成长方体,它的对角线是其外接球的直径是解题的关键.

练习册系列答案
相关题目
9.已知集合M={a|cosα<sinα,0≤α≤2π},N={α|tanα<sinα},那么M∩N是( )
| A. | ($\frac{π}{2}$,π) | B. | ($\frac{π}{4}$,$\frac{3π}{4}$) | C. | (π,$\frac{3π}{2}$) | D. | ($\frac{3π}{4}$,$\frac{5π}{4}$) |
6.设二项式(x-y)m(m∈N*)的展开式中,x4yr的系数为-35,则(2x+$\frac{1}{2\sqrt{x}}$)r+3的展开式中,常数项为( )
| A. | $\frac{21}{2}$ | B. | $\frac{15}{4}$ | C. | 10 | D. | 5 |
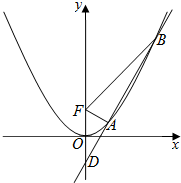 已知抛物线C:x2=4y的焦点为F,过点D(0,-1)的直线l与抛物线C交于不同的A、B两点.
已知抛物线C:x2=4y的焦点为F,过点D(0,-1)的直线l与抛物线C交于不同的A、B两点.