题目内容
【题目】如图,在四棱锥S-ABCD中,底面ABCD是菱形,![]() ,
,![]() 为等边三角形,G是线段SB上的一点,且SD//平面GAC.
为等边三角形,G是线段SB上的一点,且SD//平面GAC.
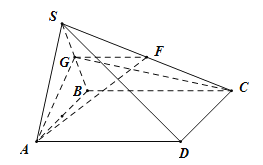
(1)求证:G为SB的中点;
(2)若F为SC的中点,连接GA,GC,FA,FG,平面SAB⊥平面ABCD,![]() ,求三棱锥F-AGC的体积.
,求三棱锥F-AGC的体积.
【答案】(1)见解析;(2)![]()
【解析】
![]() 连接
连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,利用线面平行的性质定理可得,
,利用线面平行的性质定理可得,![]() //
//![]() ,再由
,再由![]() 为
为![]() 的中点即可得证;
的中点即可得证;
![]() 利用边长的倍数关系和棱锥的体积公式
利用边长的倍数关系和棱锥的体积公式![]() 进行转化,
进行转化, ![]()
![]()
![]() ,利用间接法,结合题意求出
,利用间接法,结合题意求出![]() 即可.
即可.
(1)证明:如图,连接![]() 交
交![]() 于点
于点![]() ,则
,则![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,
∵![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() ,而
,而![]() 为
为![]() 的中点,∴
的中点,∴![]() 为
为![]() 的中点.
的中点.
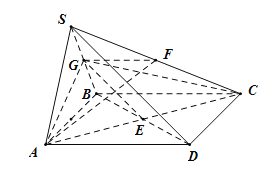
(2)解:∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴![]()
![]()
![]() .
.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵![]() 为等边三角形,∴
为等边三角形,∴![]() ,
,
又平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
因为![]() ,所以
,所以![]() ,因为
,因为![]() ,
,
∴![]()
![]() ,
,
∴![]() .
.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目

