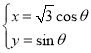题目内容
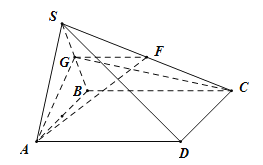
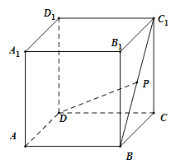
【题目】如图,三棱锥![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 的平分线
的平分线![]() ,且棱锥的三个侧面与底面都成
,且棱锥的三个侧面与底面都成![]() 角,求棱锥的侧面积与体积.
角,求棱锥的侧面积与体积.

【答案】![]() 侧
侧![]() ;
;![]()
【解析】
设![]() ,由
,由![]() 得到
得到![]() ,及
,及![]() ,顶点在底面上的射影为
,顶点在底面上的射影为![]() 的内心,由余弦定理得到BC,进一步算得
的内心,由余弦定理得到BC,进一步算得![]() 内切圆半径,进一步得到
内切圆半径,进一步得到![]() 到底面距离为
到底面距离为![]() ,以及
,以及![]() ,再利用侧面积、体积公式运算即可.
,再利用侧面积、体积公式运算即可.
在底面![]() 中,设
中,设![]() ,则
,则![]() ,
,
所以![]()
即![]() ,
,
![]() ,又
,又![]() ,
,
所以![]() ,从而
,从而![]() ,
,
![]() .
.
过P作![]() 平面ABC,过O分别作
平面ABC,过O分别作![]() ,
,
连接![]() ,又
,又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,所以
,所以![]() ,同理
,同理![]() ,
,
所以![]() 、
、![]() 、
、![]() 为三个侧面与底面都成的角,
为三个侧面与底面都成的角,
且大小等于![]() ,
,![]() ,所以
,所以![]() 为
为![]() 内心,
内心,
则![]() 在
在![]() 上,设
上,设![]() ,则
,则![]() (
(![]() 为
为![]() 内切圆半径).
内切圆半径).
在![]() 中,
中,![]() ,
,
由余弦定理,得![]()
![]() ,所以
,所以![]() ,
,
设![]() 为
为![]() 的半周长,则
的半周长,则
![]() ,∴
,∴![]() ,
,
![]()
![]() ,
,
![]() 侧
侧![]()
![]()
∴![]() .从而
.从而![]() .
.

【点晴】
本题主要考查锥体的体积及侧面积的计算,涉及到面积射影定理、余弦定理的应用,考查学生的数学运算能力,空间想象能力,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目