题目内容
3.设由不等式$\left\{\begin{array}{l}{x+y-1≥0}&{\;}\\{x-y+1≥0}&{\;}\\{2x-y-2≤0}&{\;}\end{array}\right.$表示的平面区域为4,若直线kx-y+1=0(k∈R)平分A的面积,则实数k=$\frac{1}{2}$.分析 确定三条直线的交点坐标,根据直线kx-y+1=0过(0,1),若其将三角形ABC分为面积相等的两部分,只需将线段BC平分即可,求出BC的中点的坐标代入kx-y+1=0,即可求得k的值.
解答 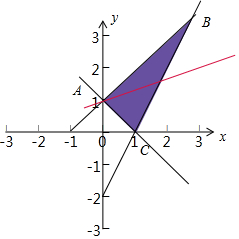 解:由题意,直线l1:x-y+1=0与直线l2:x+y-1=0的交点为A(0,1)
解:由题意,直线l1:x-y+1=0与直线l2:x+y-1=0的交点为A(0,1)
直线l1:x-y+1=0与直线l3:2x-y-2=0的交点为B(3,4)
直线l2:x+y-1=0与直线l3:2x-y-2=0的交点为C(1,0)
直线kx-y+1=0显然过点A(0,1),若其将三角形ABC分为面积相等的两部分,只需将线段BC平分即可.
设BC的中点为D,可得D的坐标为(2,2).
代入kx-y+1=0可得k=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题考查线性规划知识,考查学生分析解决问题的能力,解题的关键是将三角形ABC分为面积相等的两部分,只需将线段BC平分即可,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
11.“直线ax+3y+3=0和直线4x+(a+1)y+4=0平行”的充要条件是“a=( )”
| A. | -4或3 | B. | -$\frac{3}{7}$ | C. | -3 | D. | -4 |
8.复数z满足z(1+i)=2i(i为虚数单位),则z的虚部为( )
| A. | 1 | B. | -1 | C. | -i | D. | i |
13.复数(i-1-i)3的虚部为( )
| A. | 8i | B. | -8i | C. | 8 | D. | -8 |
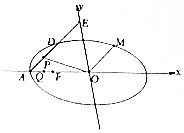 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1(a>2$\sqrt{3}$)的左焦点为F,左顶点为A,$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,其中O为原点,e为椭圆的离心率,过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{12}$=1(a>2$\sqrt{3}$)的左焦点为F,左顶点为A,$\frac{1}{|OF|}$+$\frac{1}{|OA|}$=$\frac{3e}{|FA|}$,其中O为原点,e为椭圆的离心率,过点A作斜率为k(k≠0)的直线l交椭圆C于点D,交y轴于点E.