题目内容
已知tan2θ=-2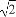
,π<2θ<2π,化简
= .
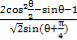3+2
【解析】原式=
=
.
∵2θ∈(π,2π),∴θ∈(
,π).
而tan2θ=
=-2.
∴tan2θ-tanθ-=0,
即(tanθ+1)(tanθ-)=0.
故tanθ=-
或tanθ=(舍去).
∴=
=3+2.
练习册系列答案
相关题目
题目内容
已知tan2θ=-2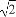,π<2θ<2π,化简= .
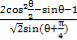3+2
【解析】原式==.
∵2θ∈(π,2π),∴θ∈(,π).
而tan2θ==-2.
∴tan2θ-tanθ-=0,
即(tanθ+1)(tanθ-)=0.
故tanθ=-或tanθ=(舍去).
∴==3+2.
