��Ŀ����
7����֪ʵ��x��y����Լ������$\left\{\begin{array}{l}x��1\\ y��x-1\\ x+y��4\end{array}\right.$��Ŀ�꺯��z=x+y����z=3ʱ��x2+y2��ȡֵ��Χ�ǣ�������| A�� | $[\frac{{3\sqrt{2}}}{2}��\sqrt{5}]$ | B�� | $[\frac{{3\sqrt{2}}}{2}��5]$ | C�� | $[\frac{9}{2}��5]$ | D�� | $[\sqrt{5}��\frac{9}{2}]$ |
���� ��������ʽ���Ӧ��ƽ����������Ŀ�꺯���ļ������壬���ɵõ�����
���  �⣺��������ʽ��Ӧ��ƽ������
�⣺��������ʽ��Ӧ��ƽ������
��Ŀ�꺯��z=x+y����z=3ʱ����x+y=3ʱ��������ʱ��ֱ�ߣ�
��x2+y2�ļ�������Ϊ����P��x��y����ԭ��ľ����ƽ����
��ֱ��x+y=3��Բx2+y2=r2����ʱ��������С��
��ԭ�㵽ֱ��x+y=3�ľ���d=$\frac{3}{\sqrt{2}}$������СֵΪd2=$\frac{9}{2}$��
��ֱ��x+y=3��Բx2+y2=r2�ཻ���B��Cʱ���������
��$\left\{\begin{array}{l}{x=1}\\{x+y=3}\end{array}\right.$�����x=1��y=2����B��1��2����ͬ�����C��2��1��
��ʱr2=x2+y2=22+12=5��
��ѡ��C��
���� ������Ҫ�������Թ滮��Ӧ�ã�����Ŀ�꺯���ļ������壬������ν�ϵ���ѧ˼���ǽ����������Ļ��������������е��⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
2����ֱ�ǡ�ABC�У���BCA=90�㣬CA=CB=1��PΪAB���ϵĵ�$\overrightarrow{AP}$=��$\overrightarrow{AB}$����$\overrightarrow{CP}$•$\overrightarrow{AB}$��$\overrightarrow{PA}$•$\overrightarrow{PB}$����˵����ֵ�ǣ�������
| A�� | $\frac{{2+\sqrt{2}}}{2}$ | B�� | $\frac{{2-\sqrt{2}}}{2}$ | C�� | 1 | D�� | $\sqrt{2}$ |
12��˫����$\frac{{x}^{2}}{m}-\frac{{y}^{2}}{4}$=1�Ľ���Ϊ6����m��ֵ�ǣ�������
| A�� | 6��2 | B�� | 5 | C�� | 1��9 | D�� | 3��5 |
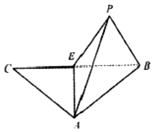 ������ABC��EΪ�ױ�BC���е㣬��AE�۵�����ͼ����C�۵���P��λ�ã�ʹ�����P-AE-C�Ĵ�СΪ120�㣬���P����ABE�ϵ���ӰΪH��
������ABC��EΪ�ױ�BC���е㣬��AE�۵�����ͼ����C�۵���P��λ�ã�ʹ�����P-AE-C�Ĵ�СΪ120�㣬���P����ABE�ϵ���ӰΪH��