题目内容
已知两点A(-1,1),B(3,3).
(1)求直线AB的方程;
(2)求线段AB的垂直平分线l的直线方程.
(1)求直线AB的方程;
(2)求线段AB的垂直平分线l的直线方程.
考点:直线的一般式方程与直线的垂直关系,直线的两点式方程
专题:直线与圆
分析:(1)由题意易得直线AB的两点式方程,化为一般式可得;
(2)可得线段AB的中点坐标,由斜率公式可得kAB,进而由垂直关系可得kl,可得l的点斜式方程,化为一般式即可.
(2)可得线段AB的中点坐标,由斜率公式可得kAB,进而由垂直关系可得kl,可得l的点斜式方程,化为一般式即可.
解答:
解:(1)∵A(-1,1),B(3,3),
∴直线AB的两点式方程为
=
,
化为一般式可得x-2y+3=0;
(2)由中点坐标公式可得线段AB的中点坐标为(1,2)
由斜率公式可得kAB=
=
∵直线AB⊥l,∴kl=-2,
∴直线l的方程为y-2=-2(x-1),
化为一般式可得2x+y-4=0
∴直线AB的两点式方程为
| y-1 |
| 3-1 |
| x-(-1) |
| 3-(-1) |
化为一般式可得x-2y+3=0;
(2)由中点坐标公式可得线段AB的中点坐标为(1,2)
由斜率公式可得kAB=
| 3-1 |
| 3-(-1) |
| 1 |
| 2 |
∵直线AB⊥l,∴kl=-2,
∴直线l的方程为y-2=-2(x-1),
化为一般式可得2x+y-4=0
点评:本题考查珍惜的一般式方程和两点式方程,涉及直线的垂直关系,属基础题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
下列两个程序(1)和(2)的运行的结果i分别是( )

| A、7,7 | B、7,6 |
| C、6,7 | D、6,6 |
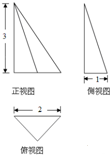 某三棱锥的三视图如图所示,其正视图和侧视图都是直角三角形,则该三棱锥的体积等于( )
某三棱锥的三视图如图所示,其正视图和侧视图都是直角三角形,则该三棱锥的体积等于( )A、
| ||
B、
| ||
| C、1 | ||
| D、3 |
如图所示,为了测量某障碍物两侧A,B间的距离,给定下列四组数据,不能确定A,B间距离的是( )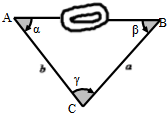

| A、α,a,b |
| B、α,β,a |
| C、a,b,γ |
| D、α,β,b |
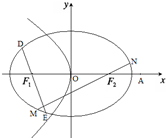 设椭圆C1:
设椭圆C1:
