题目内容
在区间[1,4]内取数a,在区间[0,3]内取数b,则函数f(x)=
x2+
x+(5-b)有两个相异零点的概率是( )
| 1 |
| 4 |
| a |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:设所求的事件为A,由方程
x2+
x+(5-b)=0有两个相异根,即△>0求出a,b范围,判断出是一个几何概型后,在坐标系中画出所有的实验结果和事件A构成的区域,再用定积分求出事件A构成的区域的面积,代入几何概型的概率公式求解.
| 1 |
| 4 |
| a |
解答:
解:设事件A={使函数f(x)=
x2+
x+(5-b)有两个相异零点},
方程
x2+
x+(5-b)=0有两个相异根,即△=a-(5-b)>0,解得a+b>5,
在[1,4]上任取实数a,在[0,3]上任取实数b,
这是一个几何概型,所有的实验结果Ω={(a,b)|1≤a≤4且 0≤b≤3};
事件A={(a,b)|a+b>5,1≤a≤4且 0≤b≤3},在坐标系中画出图形:
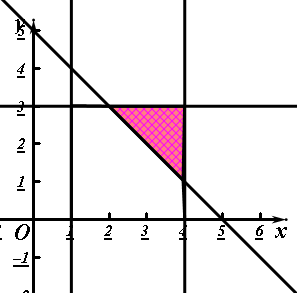
则阴影部分的面积为
×2×2=2,
∴事件A的概率P(A)=
;
故选D.
| 1 |
| 4 |
| a |
方程
| 1 |
| 4 |
| a |
在[1,4]上任取实数a,在[0,3]上任取实数b,
这是一个几何概型,所有的实验结果Ω={(a,b)|1≤a≤4且 0≤b≤3};
事件A={(a,b)|a+b>5,1≤a≤4且 0≤b≤3},在坐标系中画出图形:

则阴影部分的面积为
| 1 |
| 2 |
∴事件A的概率P(A)=
| 2 |
| 9 |
故选D.
点评:本题考查了几何概型下事件的概率的求法,用一元二次方程根的个数求出a,b的范围,用图形的面积表示事件的集合.

练习册系列答案
相关题目
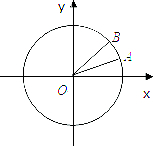 如图,在平面直角坐标系中xOy中,以轴Ox为始边做两个锐角α,β,它们的终边分别与单位圆相交于A.B两点,已知A,B的纵坐标分别为
如图,在平面直角坐标系中xOy中,以轴Ox为始边做两个锐角α,β,它们的终边分别与单位圆相交于A.B两点,已知A,B的纵坐标分别为