题目内容
5.过(2,0)点作圆(x-1)2+(y-1)2=1的切线,所得切线方程为( )| A. | y=0 | B. | x=1和y=0 | C. | x=2和y=0 | D. | 不存在 |
分析 由题意得圆心为C(1,1),半径r=1.讨论当l过点(2,0)与x轴垂直时,直线l与x轴不垂直,可设切线l的方程为y=k(x-2),根据直线l与圆相切,利用点到直线的距离公式建立关于k的等式,解出k,即可得所求切线方程.
解答 解:圆(x-1)2+(y-1)2=1的圆心为C(1,1),半径r=1.
①当直线l经过点P(2,0)与x轴垂直时,方程为x=2,
∵圆心到直线x=2的距离等于1,∴直线l与圆相切,即x=2符合题意;
②当直线l经过点P(2,0)与x轴不垂直时,设方程为y=k(x-2),即kx-y-2k=0.
∵直线l与圆(x-1)2+(y-1)2=1相切,
∴圆心到直线l的距离等于半径,即d=$\frac{|k-1-2k|}{\sqrt{1+{k}^{2}}}$=1,解之得k=0,
因此直线l的方程为y=0,
综上所述,可得所求切线方程为x=2或y=0.
故选C.
点评 本题给出圆的方程,求圆经过定点的切线方程.着重考查了点到直线的距离公式、圆的标准方程和直线与圆的位置关系等知识,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
16.在一次跳伞训练中,甲.乙两位学员各跳一次,设命题p是“甲降落在指定范围”,q是“乙降落在指定范围”,则命题“两位学员都没有降落在指定范围”可表示为( )
| A. | (¬p)∨(¬q) | B. | p∨(¬q) | C. | p∨q | D. | (¬p)∧(¬q) |
13.复数z=(3+2i)2(i为虚数单位),则在复平面上z的共轭复数$\overline z$对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
14.在△ABC中,A=60°,B=45°,$b=\sqrt{6}$,则a=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $2\sqrt{2}$ | D. | 3 |
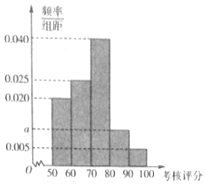 2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).
2016年,某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》,为了解本省各家企业对环保的重视情况,从中抽取了40家企业进行考核评分,考核评分均在[50,100]内,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图如图(满分为100分).