题目内容
某市调研考试后,某校对甲乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀,统计成绩后,得到如下的列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
.
(1)请完成上面的列联表
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”
参考公式与临界值表:K2=
| 3 |
| 11 |
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 合计 | 110 |
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”
参考公式与临界值表:K2=
| n(ad-bc)2 |
| (a+b)(c+d)(c+a)(b+d) |
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
考点:独立性检验的应用
专题:应用题,概率与统计
分析:(1)由于从甲、乙两个理科班全部110人中随机抽取人为优秀的概率为
,可得两个班优秀的人数,乙班优秀的人数=30-10=20,甲班非优秀的人数=110-(10+20+30)=50.即可完成表格.
(2)假设成绩与班级无关,根据列联表中的数据可得:K2,和临界值表比对后即可得到答案.
| 3 |
| 11 |
(2)假设成绩与班级无关,根据列联表中的数据可得:K2,和临界值表比对后即可得到答案.
解答:
解:(1)由于从甲、乙两个理科班全部110人中随机抽取人为优秀的概率为
.
∴两个班优秀的人数=
×110=30,
∴乙班优秀的人数=30-10=20,甲班非优秀的人数=110-(10+20+30)=50.
即可完成表格.
(2)假设成绩与班级无关K2=
=
≈7.5
则查表得相关的概率为99%,故没达到可靠性要求
| 3 |
| 11 |
∴两个班优秀的人数=
| 3 |
| 11 |
∴乙班优秀的人数=30-10=20,甲班非优秀的人数=110-(10+20+30)=50.
即可完成表格.
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | 50 | 60 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 80 | 110 |
| n(ad-bc)2 |
| (a+b)(c+d)(c+a)(b+d) |
| 110×(10×30-20×50)2 |
| 30×80×50×60 |
则查表得相关的概率为99%,故没达到可靠性要求
点评:本题考查了列联表、独立性检验,独立性检验的应用的步骤为:根据已知条件将数据归结到一个表格内,列出列联表,再根据列联表中的数据,代入公式K2,计算出k值,然后代入离散系数表,比较即可得到答案.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
双曲线
-
=1(a>0,b>0)的左、右焦点分别为F1(-c,0),F2(c,0).若双曲线上存在点P使
=
,则该双曲线的离心率的取值范围为( )
| x2 |
| a2 |
| y2 |
| b2 |
| sin∠PF1F2 |
| sin∠PF2F1 |
| a |
| c |
A、(1,
| ||||
| B、(1,2) | ||||
C、(1,
| ||||
D、(1,
|
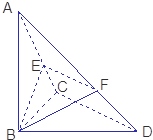 已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且