ЬтФПФкШн
вбжЊКЏЪ§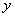 ЃН
ЃН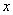 ЃЋ
ЃЋ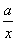 гаШчЯТаджЪЃКШчЙћГЃЪ§
гаШчЯТаджЪЃКШчЙћГЃЪ§ ЃО0ЃЌФЧУДИУКЏЪ§дк
ЃО0ЃЌФЧУДИУКЏЪ§дк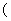 0ЃЌ
0ЃЌ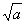
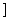 ЩЯЪЧМѕКЏЪ§ЃЌдк
ЩЯЪЧМѕКЏЪ§ЃЌдк
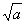 ЃЌЃЋЁо
ЃЌЃЋЁо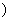 ЩЯЪЧдіКЏЪ§ЃЎ
ЩЯЪЧдіКЏЪ§ЃЎ
ЃЈ1ЃЉШчЙћКЏЪ§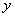 ЃН
ЃН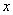 ЃЋ
ЃЋ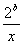 ЃЈ
ЃЈ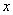 ЃО0ЃЉЕФжЕгђЮЊ
ЃО0ЃЉЕФжЕгђЮЊ 6ЃЌЃЋЁо
6ЃЌЃЋЁо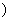 ЃЌЧѓ
ЃЌЧѓ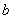 ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉбаОПКЏЪ§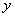 ЃН
ЃН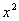 ЃЋ
ЃЋ ЃЈГЃЪ§
ЃЈГЃЪ§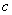 ЃО0ЃЉдкЖЈвхгђФкЕФЕЅЕїадЃЌВЂЫЕУїРэгЩЃЛ
ЃО0ЃЉдкЖЈвхгђФкЕФЕЅЕїадЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЖдКЏЪ§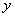 ЃН
ЃН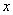 ЃЋ
ЃЋ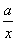 КЭ
КЭ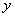 ЃН
ЃН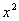 ЃЋ
ЃЋ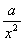 ЃЈГЃЪ§
ЃЈГЃЪ§ ЃО0ЃЉзїГіЭЦЙуЃЌЪЙЫќУЧЖМЪЧФуЫљЭЦЙуЕФКЏЪ§ЕФЬиР§ЃЎбаОПЭЦЙуКѓЕФКЏЪ§ЕФЕЅЕїадЃЈжЛаыаДГіНсТлЃЌВЛБижЄУїЃЉЁЃ
ЃО0ЃЉзїГіЭЦЙуЃЌЪЙЫќУЧЖМЪЧФуЫљЭЦЙуЕФКЏЪ§ЕФЬиР§ЃЎбаОПЭЦЙуКѓЕФКЏЪ§ЕФЕЅЕїадЃЈжЛаыаДГіНсТлЃЌВЛБижЄУїЃЉЁЃ
НтЃКЃЈ1ЃЉКЏЪ§y=x+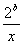 (x>0)ЕФзюаЁжЕЪЧ2
(x>0)ЕФзюаЁжЕЪЧ2 ЃЌдђ2
ЃЌдђ2 =6, Ёрb=log29.
=6, Ёрb=log29.
(2) Щш0<x1<x2,y2Ѓy1= .
.
ЕБ <x1<x2ЪБ, y2>y1, КЏЪ§y=
<x1<x2ЪБ, y2>y1, КЏЪ§y= дк[
дк[ ,+Ёо)ЩЯЪЧдіКЏЪ§ЃЛЕБ0<x1<x2<
,+Ёо)ЩЯЪЧдіКЏЪ§ЃЛЕБ0<x1<x2< ЪБy2<y1, КЏЪ§y=
ЪБy2<y1, КЏЪ§y= дк(0,
дк(0, ]ЩЯЪЧМѕКЏЪ§.гжy=
]ЩЯЪЧМѕКЏЪ§.гжy= ЪЧХМКЏЪ§ЃЌгкЪЧЃЌИУКЏЪ§дк(ЃЁо,Ѓ
ЪЧХМКЏЪ§ЃЌгкЪЧЃЌИУКЏЪ§дк(ЃЁо,Ѓ ]ЩЯЪЧМѕКЏЪ§, дк[Ѓ
]ЩЯЪЧМѕКЏЪ§, дк[Ѓ ,0)ЩЯЪЧдіКЏЪ§ЃЛ
,0)ЩЯЪЧдіКЏЪ§ЃЛ
(3) ПЩвдАбКЏЪ§ЭЦЙуЮЊy= (ГЃЪ§a>0),ЦфжаnЪЧе§ећЪ§.
(ГЃЪ§a>0),ЦфжаnЪЧе§ећЪ§.
ЕБnЪЧЦцЪ§ЪБ,КЏЪ§y= дк(0,
дк(0, ]ЩЯЪЧМѕКЏЪ§,дк[
]ЩЯЪЧМѕКЏЪ§,дк[ ,+Ёо) ЩЯЪЧдіКЏЪ§,-
,+Ёо) ЩЯЪЧдіКЏЪ§,-
дк(ЃЁо,Ѓ ]ЩЯЪЧдіКЏЪ§, дк[Ѓ
]ЩЯЪЧдіКЏЪ§, дк[Ѓ ,0)ЩЯЪЧМѕКЏЪ§
,0)ЩЯЪЧМѕКЏЪ§
ЕБnЪЧХМЪ§ЪБ,КЏЪ§y= дк(0,
дк(0, ]ЩЯЪЧМѕКЏЪ§,дк[
]ЩЯЪЧМѕКЏЪ§,дк[ ,+Ёо) ЩЯЪЧдіКЏЪ§,
,+Ёо) ЩЯЪЧдіКЏЪ§,
дк(ЃЁо,Ѓ ]ЩЯЪЧМѕКЏЪ§, дк[Ѓ
]ЩЯЪЧМѕКЏЪ§, дк[Ѓ ,0)ЩЯЪЧдіКЏЪ§.Зж
,0)ЩЯЪЧдіКЏЪ§.Зж

 ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
ЧсЫЩПЮЬУЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ ЃО10ЃЌ
ЃО10ЃЌ ЃЌдђ
ЃЌдђ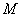 ЁЂ
ЁЂ ЕФДѓаЁЙиЯЕЪЧ
ЕФДѓаЁЙиЯЕЪЧ жаЃЌЕзУцABCЮЊжБНЧШ§НЧаЮЃЌ
жаЃЌЕзУцABCЮЊжБНЧШ§НЧаЮЃЌ ЃЌ
ЃЌ . вбжЊЃЧгыЃХЗжБ№ЮЊ
. вбжЊЃЧгыЃХЗжБ№ЮЊ КЭ
КЭ ЕФжаЕуЃЌЃФгыЃЦЗжБ№ЮЊЯпЖЮ
ЕФжаЕуЃЌЃФгыЃЦЗжБ№ЮЊЯпЖЮ КЭ
КЭ ЩЯЕФЖЏЕуЃЈВЛАќРЈЖЫЕуЃЉ. Шє
ЩЯЕФЖЏЕуЃЈВЛАќРЈЖЫЕуЃЉ. Шє ЃЌдђЯпЖЮ
ЃЌдђЯпЖЮ ЕФГЄЖШЕФзюаЁжЕЮЊ
ЕФГЄЖШЕФзюаЁжЕЮЊ  x+2|+|x+3|+
x+2|+|x+3|+ +|x+2012|+|x-1|+|x-2|+|x-3|+
+|x+2012|+|x-1|+|x-2|+|x-3|+ RЃЉЃЌЧв
RЃЉЃЌЧв дђaЕФШЁжЕЗЖЮЇЪЧ .
дђaЕФШЁжЕЗЖЮЇЪЧ .  Тњзу
Тњзу ЃЌдђ
ЃЌдђ
 гвВрЕФ
гвВрЕФ ЃЌдђКЏЪ§
ЃЌдђКЏЪ§ ЃЎ
ЃЎ
 ЃЌШє
ЃЌШє ЃЌЧв
ЃЌЧв ЃЌдђ
ЃЌдђ ЕФШЁжЕЗЖЮЇЪЧ .
ЕФШЁжЕЗЖЮЇЪЧ . 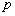 ЃКЁАШє
ЃКЁАШє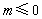 ЃЌдђ
ЃЌдђ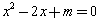 гаЪЕЪ§НтЁБЕФФцУќЬтЃЛУќЬт
гаЪЕЪ§НтЁБЕФФцУќЬтЃЛУќЬт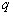 ЃКЁАШєКЏЪ§
ЃКЁАШєКЏЪ§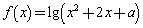 ЕФжЕгђЮЊ
ЕФжЕгђЮЊ ЃЌдђ
ЃЌдђ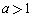 ЁБЃЎвдЯТЫФИіНсТлЃК
ЁБЃЎвдЯТЫФИіНсТлЃК ЪЧМйУќЬтЃЛЂл
ЪЧМйУќЬтЃЛЂл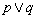 ЪЧМйУќЬтЃЛЂм
ЪЧМйУќЬтЃЛЂм ЮЊМйУќЬтЃЎ
ЮЊМйУќЬтЃЎ