题目内容
已知随机变量X～N（5，32），随机变量η=
，且η～N（μ，σ2），则（ ）
| X-2 |
| 3 |
| A、μ=1，σ=1 | ||
B、μ=1，σ=
| ||
C、μ=1，σ=
| ||
D、μ=3，σ=
|
考点：正态分布曲线的特点及曲线所表示的意义
专题：概率与统计
分析：由条件可得随机变量X的期望5和标准差3，则随机变量η的期望为
，标准差为
×3，即可得到μ，σ
| 5-2 |
| 3 |
| 1 |
| 3 |
解答：
解：∵随机变量X服从正态分布X～N（5，32），
∴可得随机变量X的期望是5，标准差为3，
∴η=
的随机变量η的期望是1，标准差为
×3=1，
故选A．
∴可得随机变量X的期望是5，标准差为3，
∴η=
| X-2 |
| 3 |
| 1 |
| 3 |
故选A．
点评：本题主要考查正态分布的均值和标准差的求法，注意应用均值和方差、标准差的公式的性质．
练习册系列答案
相关题目
函数f（x）=x
在原点处的切线方程是（ ）
| 1 |
| 3 |
| A、x=0 | B、y=0 |
| C、x=0或y=0 | D、不存在 |
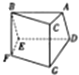如图，已知多面体ABC-DEFG中，AB、AC、AD两两垂直，平面ABC∥平面DEFG，平面BEF∥平面ADGC，AB=AD=DG=2，AC=EF=1，则下列说法中正确的个数为（ ）