题目内容
证明：
，
，
不能为同一等差数列中的三项．
，，不能为同一等差数列中的三项．见解析
假设，，为同一等差数列的三项，则存在整数m、n满足
①×n－②×m得n－m＝(n－m)，两边平方得3n2＋5m2－2
mn＝2(n－m)2，左边为无理数，右边为有理数，且有理数≠无理数，故假设不正确，即，，不能为同一等差数列的三项．
，，为同一等差数列的三项，则存在整数m、n满足①×n－②×m得
n－m＝(n－m)，两边平方得3n2＋5m2－2mn＝2(n－m)2，左边为无理数，右边为有理数，且有理数≠无理数，故假设不正确，即，，不能为同一等差数列的三项．
练习册系列答案
考前必练系列答案
相关题目
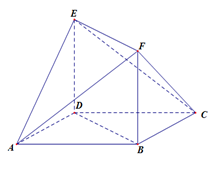
是菱形，
是矩形，
平面
，
．
平面
；
为直二面角，求直线
与平面
所成的角
的正弦值．
有有理实数根，那么
，
，
中至少有一个是偶数，下列假设中正确的是（）
＝1写出具有类似特性的性质，并加以证明．
>0,
>0,
>0,用反证法求证
>0, 
>0,c>0的假设为
不全是正数
均为实数，且
，