题目内容
15.将f(x)=sin(2x+φ)的图象向左平移$\frac{π}{8}$ 个单位后,得到的图象关于y 轴对称,则最大负数φ=-$\frac{3π}{4}$.分析 根据y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的奇偶性,求得最大负数φ.
解答 解:将f(x)=sin(2x+φ)的图象向左平移$\frac{π}{8}$ 个单位后,可得y=sin(2x+$\frac{π}{4}$+φ)的图象,
若得到的图象关于y 轴对称,则$\frac{π}{4}$+φ=kπ+$\frac{π}{2}$,即φ=kπ+$\frac{π}{4}$,k∈Z.
令k=-1,可得最大负数φ=-$\frac{3π}{4}$,
故答案为:-$\frac{3π}{4}$.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,正弦函数、余弦函数的奇偶性,属于基础题.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
5.某几何体的三视图如图所示,则此几何体的体积为( )


| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | 4 | D. | 8 |
 ,则
,则 的最大值为( )
的最大值为( )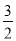 C.1 D.
C.1 D.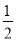
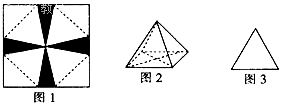 将一张边长为6cm的纸片按如图l所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是$\frac{8\sqrt{6}}{3}$.
将一张边长为6cm的纸片按如图l所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折叠并拼成一个有底的正四棱锥(底面是正方形,顶点在底面的射影为正方形的中心)模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则正四棱锥的体积是$\frac{8\sqrt{6}}{3}$.