题目内容
求下列式子是值：
log2[log3（log464）]+(
)-
-π0-lne2+lg1000．
log2[log3（log464）]+(
| 16 |
| 81 |
| 3 |
| 4 |
考点：对数的运算性质
专题：函数的性质及应用
分析：利用对数的运算法则及分数指数幂的运算法则求出值．
解答：
解：原式=log2（log33）+
-1-2+3
=0+
=
| 27 |
| 8 |
=0+
| 27 |
| 8 |
=
| 27 |
| 8 |
点评：本题考查对数的运算法则及分数指数幂的运算法则，属于一道基础题．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
从只含有二件次品的10个产品中取出三件，设A为“三件产品不全是次品”，B为“三件产品全不是次品”，C为“三件产品全是次品”，则下列结论正确的是（ ）
| A、事件A与B互斥 |
| B、事件A是随机事件 |
| C、任两个均互斥 |
| D、事件C是不可能事件 |
某家具生产厂需要在一个半径为1的圆形木料中依照图纸方式切割出如图十字图形，其中∠AEF=θ（θ为变量），AB=HG=x，AF=y．
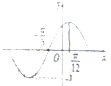函数f（x）=Asin（ωx+φ）（其中A＞0，ω＞0），|φ|≤| π |
| 2 |
A、f（x）=sin（2x+
| ||
B、f（x）=sin（2x-
| ||
C、f（x）=sin（4x+
| ||
D、f（x）=sin（4x-
|
已知函数f（x）=
，若a，b，c互不相等，且f（a）=f（b）=f（c），则abc的取值范围是（ ）
|
| A、（1，10） |
| B、（10，12） |
| C、（5，6） |
| D、（20，24） |
已知等差数列{an}满足a2+a10=4，则a6=（ ）
| A、-2 | B、2 | C、4 | D、-4 |
设全集I={0，1，2，3，4，5}，集合A={0，1，2}，集合B={2，4，5}，则∁IA∪B=（ ）
| A、{4，5} |
| B、{0，1，2，3} |
| C、{2，3，4，5} |
| D、{0，1，2，3，4，5} |