在△ABC中.a=3.b=26.∠B=2∠A.则c= ．题目和参考答案——青夏教育精英家教网—

题目内容

在△ABC中，a=3，b=2

，∠B=2∠A，则c=

．

考点：余弦定理

专题：解三角形

分析：由∠B=2∠A，得到sinB=sin2A=2sinAcosA，利用正弦定理化简将a与b的值代入求出cosA的值，利用余弦定理列出关系式，将a，b，cosA的值代入即可求出c的值．

解答： 解：∵∠B=2∠A，
∴sinB=sin2A=2sinAcosA，
利用正弦定理化简得：b=2acosA，
把a=3，b=2

代入得：2

=6cosA，即cosA=

，
由余弦定理得：a²=b²+c²-2bccosA，即9=24+c²-8c，
解得：c=5或c=3，
当c=3时，a=c，即∠A=∠C，∠B=2∠A=2∠C，
∴∠A+∠C=∠B，即∠B=90°，
而3²+3²≠（2

）²，矛盾，舍去；
则c=5．
故答案为：5

点评：此题考查了正弦、余弦定理，以及二倍角的正弦函数公式，熟练掌握定理是解本题的关键．

练习册系列答案

相关题目

下列结论中：
①当x＞0且x≠1时，lgx+

＞2的解集为（-1，0）∪（1，+∞）
正确的序号有

．

已知函数f（x）对任意x，y都有f（x+y）=f（x）+f（y）-1，且当x＞0时，f（x）＞1，若关于x的不等式f（x²-ax+b）＜1的解集为{x|-3＜x＜2}，则a+b=

自单位圆外任意一点P引圆的两条切线，切点分别为点A、B，那么

•

的最小值是

．

对任意x∈R，都有f（x+1）=f（x），g（x+1）=-g（x），且h（x）=f（x）g（x）在[0，1]上的值域[-1，2]，则h（x）在[0，2]上的值域为

．

已知复数z满足|z+1|+|z-1|=2，则|z-2-2i|最大值是

．

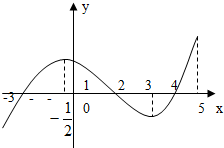如果函数y=f（x）的导函数y=f′（x）的图象如图所示，给出下列判断：
（1）函数y=f（x）在区间（4，5）内单调递增；
（2）函数y=f（x）在区间（-

，2）内单调递增；
（3）当x=-

时，函数y=f′（x）有极大值；
（4）当x=2时，函数y=f（x）有极小值．
则上述判断中不正确的是

．

试题分类