题目内容
由1,2,3,4能组成被3整除且没有重复数字的三位数的个数是( )
| A、6个 | B、12个 |
| C、18个 | D、24个 |
考点:排列、组合及简单计数问题
专题:排列组合
分析:由题意可知,能被被3整除且没有重复数字的三位数,则数字之和一定为3的倍数,因为1+2+3=6,2+3+4=9,1+2+4=7,1+3+4=8,所以三个数字为1,2,3,或2,3,4,继而问题得以解决
解答:
解:能被被3整除且没有重复数字的三位数,则数字之和一定为3的倍数,因为1+2+3=6,2+3+4=9,所以三个数字为1,2,3,或2,3,4,
故能组成被3整除且没有重复数字的三位数的个数是2
=12.
故选:B
故能组成被3整除且没有重复数字的三位数的个数是2
| A | 3 3 |
故选:B
点评:本题考查了排列中的数字问题,数字之和一定为3的倍数时解决本题的关键,属于基础题

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
记(x+
)n的展开式中第k项的系数为ak,若a3=4a5,则n=( )
| 2 |
| x |
| A、4 | B、5 | C、6 | D、7 |
某舞台灯光设计师为了在地板上设计图案,他把一端向下发光的光源和支架之间的角度固定为θ角,支架的一端固定在地板的中心位置,支架的另一端固定在天花板的适当位置,当光源围绕支架以θ角快速旋转时,地板上可能出现的图案有( )
| A、椭圆 | B、抛物线 |
| C、圆 | D、以上均有可能 |
曲线
+
=1与曲线
+
=1(k<9)的( )
| x2 |
| 25 |
| y2 |
| 9 |
| x2 |
| 25-k |
| y2 |
| 9-k |
| A、长轴长相等 | B、短轴长相等 |
| C、离心率相等 | D、焦距相等 |
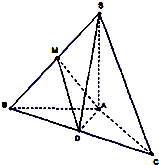 如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=
如图,在三棱锥S-ABC中,SA⊥平面ABC,AB=AC=1,SA=2,D为BC的中点.M为SB上的点,且AM=