题目内容
设函数f(x)=ax- ,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
,曲线y=f(x)在点(2,f(2))处的切线方程为7x-4y-12=0.
(1)求y=f(x)的解析式;
(2)证明:曲线y=f(x)上任一点处的切线与 直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
直线x=0和直线y=x所围成的三角形面积为定值,并求此定值.
(1)解析:方程7x-4y-12=0可化为y=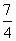 x-3,当x=2时,y=
x-3,当x=2时,y= .又f′
.又f′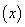 =a+
=a+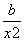 ,于是
,于是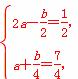 解得
解得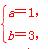 故f
故f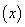 =
=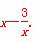
(2)证明:设P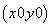 为曲线上任一点,
为曲线上任一点,
由y′=1+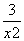 知,曲线在点P
知,曲线在点P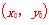 处的切线方程为
处的切线方程为
y-y0 =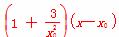 ,
,
即y-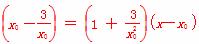 ,
,
令x=0,得y=-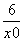 ,从而得切线与直线x=0的交点坐标为
,从而得切线与直线x=0的交点坐标为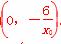 .
.
令y=x,得y=x=2x0,从而得切线与直线y=x的交点坐标为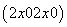 .
.
所以点P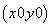 处的切线与直线x=0,y=x所围成的三角形面积为
处的切线与直线x=0,y=x所围成的三角形面积为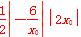 =6.
=6.
故曲线y=f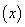 上任一点处的切线与直线x=0,y=x所围成的三角形面积为定值,此定值为6.
上任一点处的切线与直线x=0,y=x所围成的三角形面积为定值,此定值为6.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 ; ②y=axm(a,m为非零常数,且a≠1);
; ②y=axm(a,m为非零常数,且a≠1); +x2; ④y=xn; ⑤y=(x-1)3;
+x2; ④y=xn; ⑤y=(x-1)3;
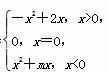 是奇函数.
是奇函数. a,a2)(a>0)处的切线与两个坐标轴围成的三角形的面积为2,则a等于( )
a,a2)(a>0)处的切线与两个坐标轴围成的三角形的面积为2,则a等于( ) D.
D.
 =cos x在
=cos x在 内( )
内( ) 有一个根
有一个根 根
根 .
.
 -
-
 -(
-(
 -1)0=( )
-1)0=( ) C.-45 D.-40
C.-45 D.-40